跨年限时任务 >> 正在进行中，欢迎大家在本帖下分享题解、代码和解题思路，你将有机会获得力扣送出的新年礼物。

下面就一起来看看今天的题目吧！

## Q69 蓝白歌会 请大家回想一下每年年终的“红白歌会” 。为分出红组和白组的胜负，野鸟会的工作人员会负责统计观众举起的红色和白色卡片的张数，这一幕大多数日本人都很熟悉（由于本书印刷颜色的关系，这里改为蓝白歌会）。

如果蓝色和白色的卡片分布过于分散，就不便于统计。因此为使结果一目了然，需要对人群进行移动调整（如果蓝色和白色人数相等，则最终两个人群之间会形成纵向或横向的分界线）。不过每次只能移动两人，并且只能是纵向或横向相邻的两人交换位置。

反复交换位置，使人群最终变为如图 1 ①中“终止状态”的 4 种状态之一。求以最少步骤由起始状态变为 4 种终止状态之一时，移动次数最多的起始状态。

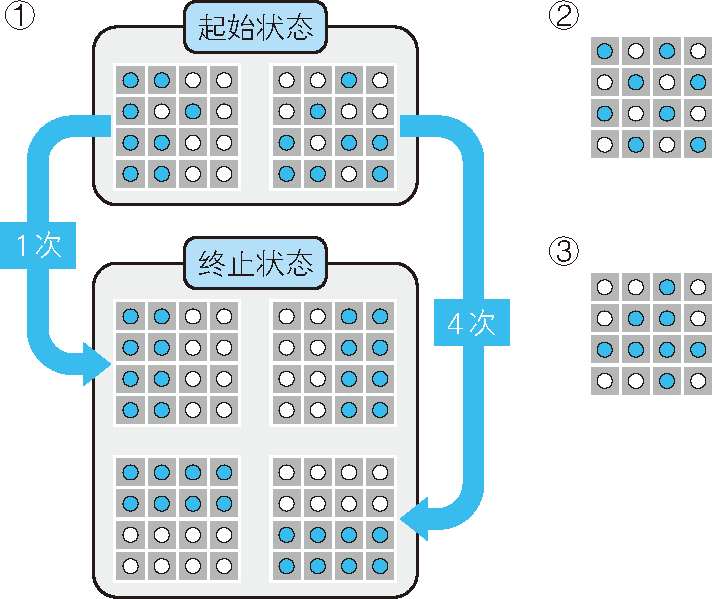
图 1 蓝色和白色的移动示例

举个例子，假设有 4×4，即 16 个人，以 8 人为一组分为两组。他们的起始状态如 ② 所示时，移动次数为 8；起始状态如 ③ 所示时，移动次数为 10。这种情况下，移动次数最多为 10，并且像 ③ 这样的起始状态有 64 种（蓝色和白色对换，以及左右对换等情况也算不同的状态）。

提问：当有 6×4，即 24 个人，以 12 人为一组分为两组时，求移动次数最多时的起始状态有多少种？

---

「跨年限时任务」活动规则

12.24 - 12.31 期间完成 跨年限时任务 >> 将有机会点亮你的「2020 年度勋章」，参与每日任务讨论还能额外获得丰厚奖励～

一、完成跨年任务，点亮年度勋章

### 二、讨论每日任务，赢丰厚奖励

参与规则

1. 从 12 月 24 日至 12 月 31 日，每天 0 点会在「讨论」发布当日「跨年限时任务」中的算法题目作为讨论贴，共 8 个讨论帖。欢迎大家在对应的讨论帖下分享自己的题解、代码及解题思路。
2. 每个 主讨论帖下点赞数前 5 的回帖可获得奖励，共 40 个奖励名额。回帖点赞统计截止日期为 2021 年 1 月 4 日 17:00。

奖励规则

• 回帖点赞第 1 名：《程序员的算法趣题》实体书 + 力扣周边盲盒 + 2020 年度实体勋章
• 回帖点赞第 2 ~ 5 名：力扣周边盲盒 + 2020 年度实体勋章

最后，别忘了在本篇讨论帖下分享「Q69 蓝白歌会」的解题思路～