二叉树是一种重要的数据结构,在计算机科学中被广泛应用,例如在搜索算法、排序算法以及数据库索引等方面,在面试中也是超高频的考点。本文会详细介绍二叉树及其遍历、构建、深度、平衡以及路径。
基本概念
在计算机科学中,二叉树(英语:Binary tree)是每个节点最多只有两个分支(即不存在分支度大于2的节点)的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序,不能随意颠倒。
二叉树的节点定义通常包含一个数据元素以及指向左右子节点的指针。以下是一个简单的二叉树节点类的示例(以 Java 为例):
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int val) {
this.val = val;
}
}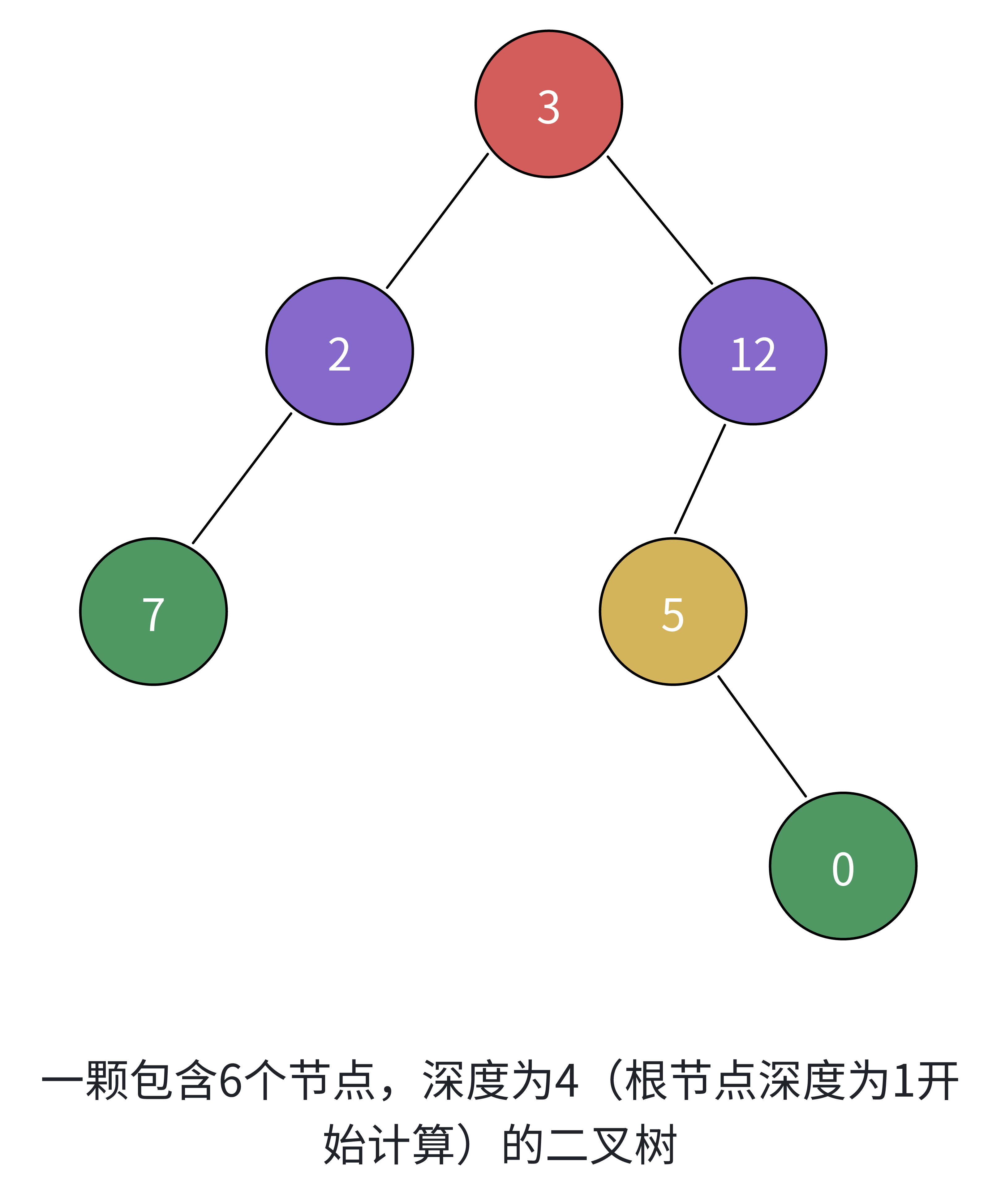
满二叉树:在一颗二叉树中,除了叶节点外,每个节点都有 2 个子节点。

完全二叉树:在一颗二叉树中,若除最后一层外的其余层都是满的,并且最后一层要么是满的,要么在右边缺少连续若干节点。以根节点深度为 1 计算,具有 n 个节点的完全二叉树的深度为 logn + 1。深度为 k 的完全二叉树,至少有2^(k - 1) 个节点,至多有 2^k - 1 个节点。

二叉树的遍历
- 前序遍历:先访问根节点,然后遍历左子树,最后遍历右子树。
- 中序遍历:先遍历左子树,然后访问根节点,最后遍历右子树。
- 后序遍历:先遍历左子树,然后遍历右子树,最后访问根节点。
- 层序遍历:自上而下,从左往右,逐层遍历
- 蛇形层序遍历(Zig-Zag 遍历):自上而下,奇偶数层,左右交替,逐层遍历。
记忆小技巧:
- 前序,中序,后序说的是根节点何时遍历;前序:根节点先;中序:根节点“居中”;后序:根节点最后;
- 左节点始终先于右节点

二叉树的前序,中序和后序遍历通常有两种方法可以实现:递归和迭代。(非常建议不熟悉递归概念的小伙伴先学习我之前写的分享 递归详解)下面我们分别来看这两种方法是如何实现的,先看递归。
递归的思路非常简单,代码也是非常简洁。以前序为例,我们先访问根节点,再左,最后右。递归的写法如下
// 前序遍历
public void preOrderTraversal(TreeNode root) {
if (root == null) {
return;
}
System.out.print(root.val + " "); // 也可以使用相应的数据结构进行存储,这里我们选择打印
preOrderTraversal(root.left);
preOrderTraversal(root.right);
}同理,中序和后序遍历的递归写法,分别为
// 中序遍历
public void inOrderTraversal(TreeNode root) {
if (root == null) {
return;
}
inOrderTraversal(root.left);
System.out.print(root.val + " "); // 也可以使用相应的数据结构进行存储,这里我们选择打印
inOrderTraversal(root.right);
}// 后序遍历
public void postOrderTraversal(TreeNode root) {
if (root == null) {
return;
}
postOrderTraversal(root.left);
postOrderTraversal(root.right);
System.out.print(root.val + " "); // 也可以使用相应的数据结构进行存储,这里我们选择打印
}递归前中后序遍历的时间复杂度和空间复杂度相同,为
时间复杂度:O(n),每个节点均被访问一次
空间复杂度:O(h), h 为树的高度,为递归栈调用的空间;如果我们需要存储节点或者节点的值到数组或者List, 则空间复杂度为O(n)
写完递归,再看迭代,用迭代的方法完成树的遍历需基于以下两点:
- 基于栈模拟递归:递归实现树的遍历本质上是利用了函数调用栈。当采用迭代方法时,使用栈数据结构来模拟函数调用栈的行为。因为栈具有后进先出(LIFO)的特性,这与递归过程中函数调用和返回的顺序相匹配。
- 对节点访问顺序的控制:在遍历过程中,根据前序、中序、后序遍历各自对节点访问顺序的要求,通过调整节点进栈和出栈的顺序来实现不同的遍历方式。
前序遍历
迭代解法基本步骤:
- 首先将根节点压入栈中。
- 当栈不为空时,执行以下操作:
- 弹出栈顶元素,访问该元素(将该元素存储至List)。
- 先将右子节点压入栈(如果存在),再将左子节点压入栈(如果存在)。这样保证在弹出时先处理左子树再处理右子树。

代码(Java)
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
Deque<TreeNode> stack = new LinkedList<>();
stack.offerLast(root);
while (!stack.isEmpty()) {
TreeNode current = stack.pollLast();
result.add(current.val);
if (current.right!= null) {
stack.offerLast(current.right);
}
if (current.left!= null) {
stack.offerLast(current.left);
}
}
return result;
}
中序遍历
迭代解法基本步骤:
- 从根节点开始,将当前节点以及其所有左子节点依次压入栈中。
- 当前节点不为空或者栈不为空时:
- 弹出栈顶元素,访问该元素。
- 将当前节点设置为弹出节点的右子节点,然后重复将当前节点及其左子节点压入栈的操作。

代码(Java)
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
Deque<TreeNode> stack = new LinkedList<>();
TreeNode current = root;
while (current != null || !stack.isEmpty()) {
if (current != null) {
stack.offerLast(current);
current = current.left;
} else {
current = stack.pollLast();
result.add(current.val);
current = current.right;
}
}
return result;
}后序遍历
迭代解法基本步骤:
- 将根节点压入栈中。
- 当栈不为空时:
- 查看栈顶元素,如果该元素满足以下三种情况之一,将其从栈中弹出并存储:
- 该元素左右子树为空
- 该元素从左子树返回 (这里无需考虑当前元素有无右子树,若无,容易理解,访问完左子树,再访问当前节点;若有,则之前该元素的左右子树均已压入栈中:当前 | 右节点 | 左节点,不存在从左节点直接回到当前节点,因为中间有右节点需要访问,最终会从右节点返回。这里也证明,直接从左节点回来的,当前节点无右节点)
- 该元素从右子树返回
- 若不满足以上的条件,说明还有其他节点需要先遍历,分别将右节点(若有),左节点(若有)压入栈中
- 查看栈顶元素,如果该元素满足以下三种情况之一,将其从栈中弹出并存储:

代码(Java)
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
if (root == null) {
return result;
}
Deque<TreeNode> stack = new LinkedList<>();
TreeNode current = root;
TreeNode pre = null;
stack.offerLast(current);
while (!stack.isEmpty()) {
current = stack.peekLast();
if ((current.left == null && current.right == null) ||
(pre != null && pre == current.left) ||
(pre != null && pre == current.right)) {
result.add(current.val);
stack.pollLast();
pre = current;
} else {
if (current.right != null) {
stack.offerLast(current.right);
}
if (current.left != null) {
stack.offerLast(current.left);
}
}
}
return result;
}迭代前中后序遍历的时间复杂度和空间复杂度相同,为
时间复杂度:O(n),每个节点均被访问一次
空间复杂度:O(h), h 为树的高度,为栈的空间;如果我们需要存储节点或者节点的值到数组或者List, 则空间复杂度为O(n)
层序遍历
树的层序遍历是一种对树进行遍历的方式,它按照树的层次依次访问每个节点。

层序遍历的核心在于按照树的层次来访问节点,这与深度优先遍历(如前序、中序、后序遍历)不同。实现层序遍历的关键是要有一种机制,能够记录并按顺序访问同一层的节点,然后再访问下一层。
- 使用队列(Queue)数据结构:
- 队列是一种先进先出(FIFO)的数据结构,非常适合按顺序存储和访问节点。
- 将根节点加入队列,在取出队列的节点之前,记录当前层节点总数,从而实现层与层的遍历,避免两层之间混淆。
- 按层处理节点:
- 每次从队列中取出一个节点,访问该节点的值。
- 将该节点的子节点(左、右子节点)按顺序加入队列。
- 由于子节点被加入队列的顺序与父节点被处理的顺序相对应,确保了节点按层次被访问。
- 循环迭代:
- 重复上述过程,直到队列为空,即所有节点都被访问过。
public List<List<Integer>> printNodes(TreeNode root) {
List<List<Integer>> result = new ArrayList<>();
if (root == null) {
return result;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
int size = queue.size();
List<Integer> curResult = new ArrayList<>();
while (size-- > 0) {
TreeNode cur = queue.poll();
curResult.add(cur.value);
if (cur.left != null) {
queue.offer(cur.left);
}
if (cur.right != null) {
queue.offer(cur.right);
}
}
result.add(curResult);
}
return result;
}时间复杂度:O(n), n 为节点的个数
空间复杂度:O(n)
蛇形层序遍历(Zig-zag 遍历)
树的蛇形层序遍历是一种特殊的树的遍历方式,它在进行层序遍历的基础上,按照层次交替改变遍历的方向,类似蛇形的行进方式。

思路:使用双端队列,奇数层从Last取,从右子树到左子树依次往First端存;偶数层从First端取,从左至右依次往Last端存。
public List<Integer> snakeTraversal(TreeNode root) {
List<Integer> result = new ArrayList<>();
Deque<TreeNode> deque = new LinkedList<>();
deque.offerLast(root);
int level = 0;
while (!deque.isEmpty()) {
int size = deque.size();
level++;
while (size > 0) {
TreeNode cur;
if (level % 2 == 0) {
cur = deque.pollFirst();
if (cur.left != null) {
deque.offerLast(cur.left);
}
if (cur.right != null) {
deque.offerLast(cur.right);
}
} else {
cur = deque.pollLast();
if (cur.right != null) {
deque.offerFirst(cur.right);
}
if (cur.left != null) {
deque.offerFirst(cur.left);
}
}
size--;
result.add(cur.value);
}
}
return result;
}时间复杂度:O(n), n 为节点的个数
空间复杂度:O(n)
二叉树的构建
根据给定的遍历序列构建二叉树,比如根据前序遍历和中序遍历序列,或者后序遍历和中序遍历序列。解法关键在于利用遍历序列的特点找到根节点在序列中的位置,从而划分左右子树的序列,递归构建。
Leetcode 105 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
思路分析:

代码
public TreeNode buildTree(int[] preorder, int[] inorder) {
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < inorder.length; i++) {
map.put(inorder[i], i);
}
return buildTree(preorder, inorder, 0, preorder.length - 1, 0, inorder.length - 1, map);
}
private TreeNode buildTree(int[] preorder, int[] inorder, int preStart, int preEnd, int inStart, int inEnd, Map<Integer, Integer> map) {
if (preStart > preEnd || inStart > inEnd) {
return null;
}
TreeNode root = new TreeNode(preorder[preStart]);
int indexOfRootInInorder = map.get(preorder[preStart]);
root.left = buildTree(preorder, inorder, preStart + 1, preStart + indexOfRootInInorder - inStart, inStart, indexOfRootInInorder - 1, map);
root.right = buildTree(preorder, inorder, preStart + indexOfRootInInorder - inStart + 1, preEnd, indexOfRootInInorder + 1, inEnd, map);
return root;
}时间复杂度:O(n)
空间复杂度:O(n)
Leetcode 106 从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
思路分析:同上,主要的区别在于,根节点的位置在后序遍历数组中的最后一个,确定了根节点的位置再根据中序遍历确定左右子树的区间,再递归求解
public TreeNode buildTree(int[] inorder, int[] postorder) {
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < inorder.length; i++) {
map.put(inorder[i], i);
}
return buildTree(inorder, postorder, 0, inorder.length - 1, 0, postorder.length - 1, map);
}
private TreeNode buildTree(int[] inorder, int[] postorder, int inStart, int inEnd, int postStart, int postEnd, Map<Integer, Integer> map) {
if (inStart > inEnd || postStart > postEnd) {
return null;
}
TreeNode root = new TreeNode(postorder[postEnd]);
int indexOfRootInInorder = map.get(postorder[postEnd]);
root.left = buildTree(inorder, postorder, inStart, indexOfRootInInorder - 1, postStart, postStart + indexOfRootInInorder - 1 - inStart, map);
root.right = buildTree(inorder, postorder, indexOfRootInInorder + 1, inEnd, postStart + indexOfRootInInorder - inStart, postEnd - 1, map);
return root;
}时间复杂度:O(n)
空间复杂度:O(n)
二叉树的深度
Leetcode 104 二叉树的最大深度
题目描述:给定一个二叉树,找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
思路分析:
对于二叉树的最大深度问题,我们可以采用递归的方法来求解。二叉树的最大深度定义为根节点到最远叶子节点的最长路径上的节点数。递归计算左子树和右子树的最大深度,然后取两者中的较大值,再加上 1(根节点这一层)就是整个二叉树的最大深度。递归的基本情况是当节点为 null 时,此时深度为 0,表示已经到达叶子节点的下一层(空节点层)。
代码:
public int maxDepth(TreeNode root) {
if (root == null) {
return 0;
}
int leftDepth = maxDepth(root.left);
int rightDepth = maxDepth(root.right);
return Math.max(leftDepth, rightDepth) + 1;
}时间复杂度:O(n), 每个节点访问一次
空间复杂度:O(h), h 为树的高度,如果树为完全二叉树或接近于完全二叉树,h = logn。空间复杂度主要来自于递归栈的调用
二叉树的平衡
- 题目描述
- 给定一个二叉树,判断它是否是高度平衡的二叉树。高度平衡二叉树定义为:一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1。
- 思路分析
- 递归计算高度并检查平衡
- 可以使用递归的方法来解决这个问题。对于每个节点,需要计算其左子树和右子树的高度,然后判断该节点是否平衡(即左右子树高度差的绝对值不超过 1)。如果有一个子树不平衡,则整个二叉树不平衡。
- 如果一个节点是平衡的,还需要递归地检查其左右子树是否也是平衡的。
- 具体实现步骤
- 首先定义一个辅助函数来计算二叉树的高度。对于一个节点,其高度为其左子树高度和右子树高度中的最大值加 1(空树高度为 0)。
- 然后自下而上递归地检查左右子树是否平衡,若平衡,返回当前子树的高度;若不平衡,返回 -1 进行标记。
- 递归计算高度并检查平衡
public boolean isBalanced(TreeNode root) {
return treeHeight(root) >= 0;
}
private int treeHeight(TreeNode root) {
if (root == null) {
return 0;
}
int leftHeight = treeHeight(root.left);
int rightHeight = treeHeight(root.right);
if (leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) > 1) {
return -1;
}
return Math.max(leftHeight, rightHeight) + 1;
}时间复杂度:O(n), 每个节点访问一次
空间复杂度:O(h), h 为树的高度,如果树为完全二叉树或接近于完全二叉树,h = logn。空间复杂度主要来自于递归栈的调用
二叉树的路径
问题描述:给定一个二叉树,返回从一个叶子节点到另一个叶子节点最大路径的和。

问题分析:
解决树的路径问题需要考虑三个核心问题:
- 你需要左右子树给你什么信息
- 当前节点拿到左右子树的信息,如何处理,返回有用的信息给上一层
- 重复1, 2, 何时停止
以上的三个问题对应递归三要素的基准、分解以及求解。那我们分别来回答以上的核心问题
- 你需要左右子树给你什么信息
需要从左子树拿到最大的单边路径,同理,需要从右子树拿到最大的单边路径。
备注:何为单边路径,从叶子节点到另一个叶子节点组成的路径会汇聚一个节点。例如路径:1 - 1 - 2 - 3 - 5。其中1 - 1 和 5 - 3都为单边路径,他们汇聚于节点2 - 当前节点拿到左右子树的信息,如何处理,返回有用的信息给上一层
a. 如果左右子树都存在单边路径,再加上当前的节点,那就组合成了一个从叶节点到另一个叶节点的路径,更新结果
b. 然后再将当前的节点拼接到左右路径较大的单边路径组合成一个新的单边路径,返回给上一层。(告诉父节点:这是到我这为止的最大单边路径,需要的话可以拿去用) - 何时停止
当节点为空的时候,返回0;0的值也不会影响如果有负数的结果,因为在上一层可以判断左右子树是否为空,从而判断是否返回了单边路径。
代码
public int maximumLeavesPath(TreeNode root) {
int[] res = {Integer.MIN_VALUE};
findLargestPath(root, res);
return res[0];
}
private int findLargestPath(TreeNode root, int[] res) {
if (root == null) {
return 0;
}
int leftLargestPath = findLargestPath(root.left, res);
int rightLargestPath = findLargestPath(root.right, res);
if (root.left != null && root.right != null) {
// 如果左右子树都不为空,说明找到一条从叶子节点到另一个叶子节点的路径,更新结果
res[0] = Math.max(res[0], leftLargestPath + rightLargestPath + root.value);
// 从左右子树中挑一个更大的路径,加上当前节点的值,返回给上一层 (告诉父节点:这是到我这为止的最大单边路径)
return root.value + Math.max(leftLargestPath, rightLargestPath);
}
// 如果左边为空,选右边的(如果右边也为空,rightLargestPath 也为0,不影响结果);如果右边为空,选左边的;
// 再加上自己,组成一条新的单边路径,返回给上一层 (告诉父节点:这是到我这为止的最大单边路径)
return root.left == null ? rightLargestPath + root.value : leftLargestPath + root.value;
}图解

时间复杂度和空间复杂度
假设这个二叉树有 n 个节点
时间复杂度为O(n), 因为每个节点都访问了一次,每次访问都是常数级操作。
空间复杂度主要来自递归栈的调用,而递归的深度取决于树的高度,n个节点的树,最差情况的高度为n, 树的每一层只有一个节点,看似一条直线,此时来自栈的空间复杂度为O(n)。如果是完全二叉树高度约为O(logn), 来自栈调用的空间复杂度为O(logn)。综上,最差情况的栈空间复杂度为O(n)。

