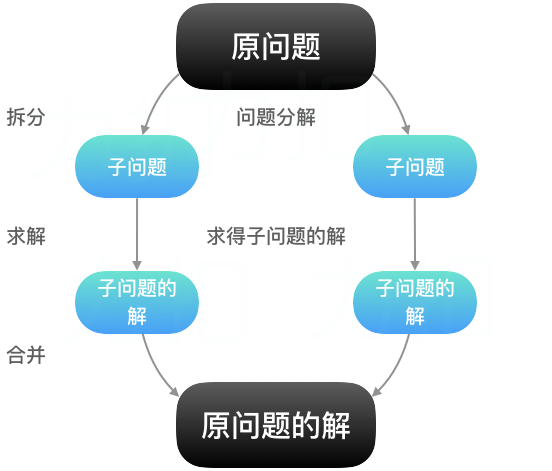
分而治之(Divide-and-Conquer)的思想分为如下三步:
拆分:将原问题拆分成若干个子问题;
解决:解决这些子问题;
合并:合并子问题的解得到原问题的解
第 2 步「解决这些子问题」不是逐个解决。是以一种「深度优先」或者说「递归」的方式解决某个子问题,等到该子问题解决完成以后,在解决同一层的其它子问题。
使用「递归」实现的算法需要走完下面两条路径:
先「自顶向下」拆分问题,直到不能拆分为止;
再「自底向上」逐层把底层的结果向上汇报,直至得到原问题的解。
因此使用「递归」函数解决的问题如上图所示,有「先走出去,再走回来」的过程。
「分治」是思想,「减治」是分治的特例;
「递归」是代码表现形式;
「递归」有先拆分问题的过程,真正解决问题,需要在拆分到底以后,一层一层向上返回。
写出递归终止条件(易忽略)
首先写出递归终止条件,也就是先写出不能再拆分的子问题。
有些朋友在初学的时候,由于忘记编写递归终止条件而导致递归调用栈满,解释器抛出 StackOverflowError 异常。
将原问题拆分成为规模更小的子问题(重点)
这一步是编写递归函数的关键,如何拆分子问题是我们需要关注的重点。
这里列出我们经常用到的拆分方式:(直接体现在递归函数的入参上)
a) 问题规模折半,即拆成两部分;
例如:实现pow(x,y) https://leetcode-cn.com/problems/powx-n/
例如:归并排序,将区间[l, r]一分为二,分成 [l, m] 和 [m + 1, r];
51 数组中的逆序对
https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/
315. 计算右侧小于当前元素的个数
https://leetcode-cn.com/problems/count-of-smaller-numbers-after-self/
例如:对字符串,经常是以某个点为分界线,分为左部分和右部分。
395. 至少有 K 个重复字符的最长子串
https://leetcode-cn.com/problems/longest-substring-with-at-least-k-repeating-characters/
241. 为运算表达式设计优先级
https://leetcode-cn.com/problems/different-ways-to-add-parentheses/b) 问题规模减少1;
递归乘法:https://leetcode-cn.com/problems/recursive-mulitply-lcci/
c) 如果数据结构是树的结构,拆分方式肯定是root和各个子节点;
将子问题的结果进行合并(难点)
有一些逻辑恰好是发生在递归函数调用返回以后,我们在这个时机还可以编写一些逻辑,使得我们求解原问题变得更加简单。我们在「递归函数的应用」章节会向大家介绍如何利用这个时机完成一些关键的逻辑。
分治的代码框架:
返回值 func(param1, param2)
{
//1. 递归的终止条件
if (n == 0) {
return 返回值;
}
// 2. 拆分,对应「分而治之」算法的「分」,并且一定要得到一个结果,在思考过程中,要假定这个子问题是可以正确解决的
// 用于第三步的合
temp = func(param1, param3); //分治思想, 一般是折半(param2/2),或者-1(param2 - 1)
// 3. 在递归函数调用完成以后还可以做点事情, 对应「分而治之」的「合」
ans = temp .....
return ans;
}以零钱兑换为例,就有分治的思想。
int Dfs(int *coins, int coinsSize, int amout)
{
if (amout == 0) {
return 0;
}
int currAns = INT_MAX;
int subAns = INT_MAX;
//将问题拆解成更小的子问题, 对应“分”的思想
for (int i = 0; i < coinsSize; i++) {
if (amout < coins[i]) {
continue;
}
int temp = Dfs(coins, coinsSize, amout - coins[i]);
if (temp == INT_MAX) {
continue;
}
subAns = fmin(subAns, temp);
}
//当子树中的问题解决以后,结合子树求解的结果处理当前结点,对应合并的思想
if (subAns != INT_MAX) {
currAns = subAns + 1;
}
return currAns;
}以每个运算符为界,将字符分成左部分和右部分,
- 先得到左部分的所有解,
- 再得到右部分的所有解;
- 将左部分的所有解和右部分的所有解组合起来;
int DivideAndConquer(char *expression, int outputAns[])
{
int sLen = strlen(expression);
bool findFlg = false;
int returnAns = 0;
for (int i = 0; i < sLen; i++) {
char alp = expression[i];
if (alp == '+' || alp == '-' || alp == '*') {
findFlg = true;
char left[1000] = {};
char right[1000] = {};
strncpy(left, expression, i);
strncpy(right, expression + i + 1, sLen - 1 - i);
int leftAns[10000] = {};
int rightAns[10000] = {};
int leftAnsNum = DivideAndConquer(left, leftAns); //left结果是个列表
int rightAnsNum = DivideAndConquer(right, rightAns); //right结果是个列表
for (int i = 0; i < leftAnsNum; i++) {
for (int j = 0; j < rightAnsNum; j++) {
switch (alp) {
case '+':
outputAns[returnAns] = leftAns[i] + rightAns[j];
returnAns++;
break;
case '-':
outputAns[returnAns] = leftAns[i] - rightAns[j];
returnAns++;
break;
case '*':
outputAns[returnAns] = leftAns[i] * rightAns[j];
returnAns++;
break;
}
}
}
}
}
//only digit
if (findFlg == false) {
sscanf(expression, "%d", &(outputAns[0]));
return 1;
}
return returnAns;
}「递归」方法与「分治思想」「减治思想」「深度优先遍历」「栈」有着千丝万缕的联系,在编写「递归」方法的同时,要有意识地思考它们之间的关系;
