前言
在再论二分查找模板之递归版文章中,我给出了二分查找的6种递归版模板,想必同学们已经理解了指针位置与区间开闭的关系,以及在模板中的相关代码体现,如指针终止条件,指针移步探索等等,总结出来就是一句话,实现对目标元素的无死角搜索(查找),绝对不能因为指针和区间的问题遗漏了目标元素。
但是我们发现二分查找模板三个构造因素里面还有一个没有探讨,那就是 指针的向上取整,向下取整,完整描述应该是 指针为区间端点下标和折半向下取整,区间端点下标和折半向上取整,这个位置其实就是中位数点。
中位数点
这里我们引入中位数点的概念,由于二分查找默认数组有序,中位数值一定位于序列下标中位数点处。
设区间为 ,下中位数点为 ,上中位数点为 。
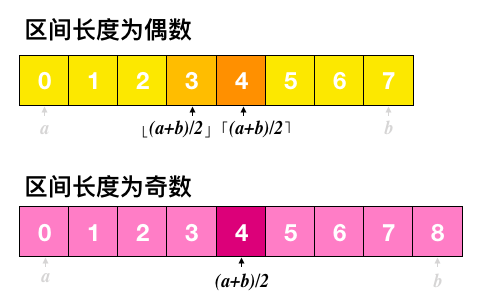
当然,区间 长度为奇数时,上中位数点与下中位数点是重合的,都位于区间中点处即 。
区间 长度为偶数时,上中位数点和下中位数点是序列中间两个点,位于中点两侧,下中位数点是小于中点且最接近中点的点处即 ,上中位数点是大于中点且最接近中点的点处即 。
我们研究下上一篇文章中的4款递归模板:
模板一:相错终止+左闭右闭类型,由于左右指针完全平等,根据轮换对称性,既然能够向下取整,就一定能够向上取整。
模板二:相等终止+左闭右开类型,始终构造左闭右开区间 ,由于取下中位数点,能够保证无论探索下一步二分探索 或者 都不会越界,极端情况是探索区间为空 表示 或者 ,一定不能出现 或者 这种非法区间,如果出现会导致程序陷入死循环。这种情况只能选取下中位数点。
模板三:相等终止+左开右闭类型,始终构造左闭右开区间 ,由于取上中位数点,能够保证无论探索下一步二分探索 或者 都不会越界,极端情况是探索区间为空 表示为 或者 ,一定不能出现 或者 这种非法区间,如果出现会导致程序陷入死循环。这种情况只能选取上中位数点。
模板四:相邻终止+左开右开类型,由于左右指针完全平等,根据轮换对称性,既然能够向下取整,就一定能够向上取整。
总结成一句话,为了保证下一次二分查找区间合法,就要选择合适的中位数点,否则会导致死循环等异常。
随机化算法
解决了上中位数点和下中位数点的问题,其实还有一个问题,为什么折半?为什么不选择三七分或者二八分?
我也不会像《算法导论》里那样进行概率数学期望计算,简单粗暴极端一点,设搜索区间长度为 ,我们每次进行 和 分,我们讨论下这种情况的最坏时间复杂度,设每次总是在左边的 进行查找且没有找到,这样分割下去就是等效于线性查找了,时间复杂度 ,但是我们如果进行二等分,时间复杂度一定稳定在 。
算法的稳定性也是算法优劣的重要评判标准。
《算法导论》第九章:中位数和顺序统计量的第二节9.2期望为线性的选择算法中提到了随机化算法(Randomized-Select),对于乱序的数组进行快速排序,实现了找中位数期望为 ,当然我们把随机化算法用在有序数组的二分查找中也是可以的,虽然似乎看起来多此一举,但是并不会增加二分查找的时间复杂度。
我们用随机化算法处理 指针,改写递归的4款模板如下:
模板一
模板简介
注意:
模板代码
class Solution {
public:
int binarySearch(vector<int>& nums, int left, int right, int target) {
if (left > right) {
return -1;
}
int offset = rand() % (right - left + 1);
int mid = left + offset;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] > target) {
return binarySearch(nums, left, mid - 1, target);
} else {
return binarySearch(nums, mid + 1, right, target);
}
}
int search(vector<int>& nums, int target) {
return binarySearch(nums, 0, (int)nums.size() - 1, target);
}
};模板二
模板简介
注意:
模板代码
class Solution {
public:
int binarySearch(vector<int>& nums, int left, int right, int target) {
if (left >= right) {
return -1;
}
int offset = rand() % (right - left);
int mid = left + offset;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] > target) {
return binarySearch(nums, left, mid, target);
} else {
return binarySearch(nums, mid + 1, right, target);
}
}
int search(vector<int>& nums, int target) {
return binarySearch(nums, 0, (int)nums.size(), target);
}
};模板三
模板简介
注意:
模板代码
class Solution {
public:
int binarySearch(vector<int>& nums, int left, int right, int target) {
if (left >= right) {
return -1;
}
int offset = rand() % (right - left);
int mid = left + 1 + offset;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] > target) {
return binarySearch(nums, left, mid - 1, target);
} else {
return binarySearch(nums, mid, right, target);
}
}
int search(vector<int>& nums, int target) {
return binarySearch(nums, -1, (int)nums.size() - 1, target);
}
};模板四
模板简介
注意:
模板代码
class Solution {
public:
int binarySearch(vector<int>& nums, int left, int right, int target) {
if (left + 1 >= right) {
return -1;
}
int offset = 1 + rand() % (right - left - 1);
int mid = left + offset;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] > target) {
return binarySearch(nums, left, mid, target);
} else {
return binarySearch(nums, mid, right, target);
}
}
int search(vector<int>& nums, int target) {
return binarySearch(nums, -1, (int)nums.size(), target);
}
};总结
其实由于二分查找的数组已经有序,随机化纯属多此一举,但是我们似乎看清了二分查找与快速排序的关系,二分查找实际上就是有序的快速排序的顺序统计量问题。
我来异想天开下,二分查找也可以结合快速排序用在乱序数组中,我们没有必要对乱序数组进行完全排序再进行二分查找,我们可以根据二分查找的二分条件进行 的局部排序然后再进行二分查找,虽然实际做题中不会这么去处理。
《算法导论》里没有章节专门研究二分查找,其实二分查找的思想就蕴藏在《算法导论》的前几章里,下期我尝试溯源下二分查找。
吐槽下,《算法导论》实在是太难了,还是力扣刷题友好。
本人才疏学浅,也是为了抛砖引玉,还请各位大佬们斧正!
