前言
字节面试一波三折,简历被刷两次,没想到能被捞起来参加笔试,更没想到能过笔试,更更没想到能过一面,现在二面等结果,虽然觉得没希望了,还是把这道题记录一下。
简介
字节二面的一道算法题,当时只想到了暴力,面试官提示了优化但是我没有get到他的点,就换了另一题,二叉树的左视图,力扣有原题,每日一也做过,就不说了,还是讨论下面这道,可能不算难吧,但是我当时确实没别的思路,朋友跟我说了才理解了面试官当时的意思。
题目
题意:
牛牛有一个苹果园。又到了一年一度的收获季,牛牛现在要去采摘苹果买给市场的摊贩们。
牛牛的果园里面有n棵苹果树,第i棵苹果树上有ai个果子。
牛牛为了保证果子的新鲜程度,每天都会去苹果树上采摘果子。牛牛特意安排一个计划表:
计划m天去采摘果子。
对于第i天,它会去所有果树上轮流采摘bi个果子。
如果对于第i天,某棵果树上没有bi个果子,那么它只会把当前果树上的果子采摘完。
牛牛想知道它每天能供应多少个苹果给市场的摊贩们。
(力扣上不清楚原题在哪,我刷的题不算多,如果有类似的题欢迎评论)
示例:
输入
[10,20,10],[5,7,2]输出
[15,17,2]说明
苹果树上的果子变化[10,20,10]-->[5,15,5]-->[0,8,0]-->[0,6,0]题解
方法一:暴力法
暴力法就是双重循环的套路。时间复杂度O(n^2)
public class Solution {
/**
* 摘苹果
*
* @param a 每棵树对应的苹果数量
* @param b 每天计划要摘的苹果数量(一棵树的计划量
* @return 每天实际能采摘的苹果数量
*/
public static long[] pickApples(int[] a, int[] b) {
int m = b.length;
int n = a.length;
long[] res = new long[m];
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (a[j] >= b[i]) {
res[i] += b[i];
a[j] -= b[i];
} else {
res[i] += a[j];
a[j] = 0;
}
}
}
return res;
}
}方法二:预排序 + 二分查找
思路
前面的暴力法我们每一天每一棵苹果树都爬上去看看苹果够不够,当时面试官跟我说的大概优化意思是:我们不用去管苹果数量够的苹果树,够的直接把他们乘起来,不够的话就要去计算。
(大概这个意思,没录音我描述的肯定不准确,毕竟当时也没get到点。
后来跟朋友@aweng说了下,他想了下就说了预排序和二分查找的思路:把苹果树按数量排好序,每次找的时候从苹果数量足够的树开始摘。然后晚上我要睡大觉的时候跟我说了完整的思路,大概这就是大佬吧,而我面试完只想好好睡一觉😴
具体实现就是在摘苹果的时候,我们不去真的摘,也就是不对苹果树进行整个遍历然后相减,相反的,我们采取对计划要摘得苹果量进行加法计算得方式。因为天数是肯定需要遍历的,所以我们可以把优化放在“摘”苹果这个动作上。
我的描述能力不太行,直接上例子来说😂。
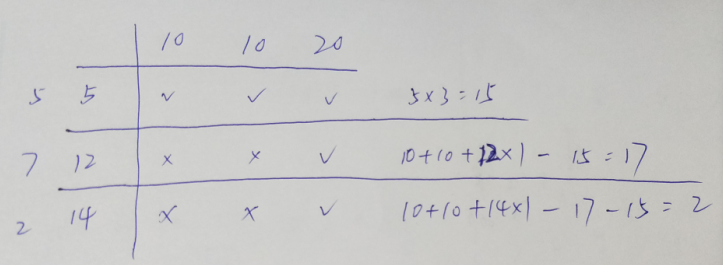
比如对 a = [10, 10, 20],b = [5, 7, 2] 来说
-
第一天每棵树要摘5个苹果,三棵树都足够,所以第一天能摘
3 × 5 = 15个苹果; -
第二天每棵树要摘7个苹果,因为我们没有对苹果树进行“摘”的操作,所以要对计划量进行“加”的操作,也就是当天计划摘
5 + 7 = 12个苹果,或者我认为也可以这么想,这相当于一个压缩操作,我们把两天的计划放到一天来执行,也就是说今天要摘12个苹果,此时,只有第三棵树符合要求,而前两棵树都会被摘空。所以今天能摘的苹果数量为:前两棵苹果的总数 + 第三棵计划摘得苹果数 - 前一天摘得苹果数,也就是10 + 10 + 12 × 1 - 15 = 17个苹果; -
第三天每棵树要摘2个苹果,压缩到一天也就是今天要摘
5 + 7 + 2 = 14个苹果,也是只有第三棵树符合要求,再加上前两棵所有的苹果数,最后减去前两天摘得苹果数,所以今天能摘的苹果数量为10 + 10 + 14 - 15 - 17 = 2个苹果。
这时候你会发现我们的预排序还没起到作用,二分查找也还没上场,其实这两者的搭配就是为了更快地找出我们“爬树”的起点 start ,满足预排序后对苹果树ai有以下两点
- i < start 的苹果树,苹果数量不足够,需要全部采摘
- i ≥ start 的苹果树,苹果数量足够,无需遍历,有多少颗就直接相乘
总结主题思路就是,当天的时候假设把计划量全压到一天来做,预排序后通过二分找起点树,前面的苹果树上的苹果依次全摘,做加法,后面的苹果上的苹果树不管,直接做乘法。加完后减去前段时间摘得苹果数,就是今天能摘得苹果总数了。
大概思路就这样了,不知道我说明白了没有,原谅我的语言表达能力。
代码实现
我们维护一个sum,来记录前几天能摘的所有苹果的数量,res[i]记录当天能摘的苹果数量,start记录起点,tmp记录今天计划要摘的苹果数量(累加后的)
@发狂的橘子 提出了前缀和的优化,已修改,他的python代码可以参考评论区。优化后时间复杂度为O(mlogn)。
public class Solution {
/**
* 摘苹果
*
* @param a 每棵树对应的苹果数量
* @param b 每天计划要摘的苹果数量(一棵树的计划量
* @return 每天实际能采摘的苹果数量
*/
public static long[] pickApples(int[] a, int[] b) {
// 天数
int m = b.length;
// 苹果树数
int n = a.length;
long[] res = new long[m];
// 预排序
Arrays.sort(a);
// 记录前缀和,pre[i]代表0~i棵树上果子数量的总和
int[] prefix = new int[n];
prefix[0] = a[0];
for (int i = 1; i < n; ++i) {
prefix[i] = prefix[i - 1] + a[i];
}
// 记录前几天总共摘到的苹果数量
int sum = 0;
// 记录从第几棵苹果树开始摘
int start = 0;
// 累加到当天的计划每棵树要摘的苹果数量
int tmp = 0;
for (int i = 0; i < m; ++i) {
// 更新计划要摘的苹果数量
tmp += b[i];
// 寻找新的起点
start = binarySearch(a, start, tmp);
// 足够的直接乘 + 不足的全摘光 - 前几天摘的
res[i] = (n - start) * tmp + (start > 0 ? prefix[start - 1] : 0) - sum;
// 更新摘下的苹果总数量
sum += res[i];
}
return res;
}
/**
* 二分寻找起点,这个起点意味着包括自身在内及以后的苹果树的数量都是足够被采摘的
*
* @param num 苹果树
* @param start 原起点,因为预排序过后,前一天不够摘的苹果树后一天肯定也足够,所以可以直接以上一轮的start为起点
* @param target 计划要摘的苹果数量
* @return 大于等于target的数所对应的下标
*/
private static int binarySearch(int[] num, int start, int target) {
if (target > num[num.length - 1]) {
return num.length;
}
if (target < num[0]) {
return 0;
}
int l = start, r = num.length - 1;
while (l < r) {
int mid = l + (r - l >> 1);
if (num[mid] >= target) {
r = mid;
} else if (num[mid] < target) {
l = mid + 1;
}
}
return l;
}
}
方法三:双指针
评论区大佬的解法,可以移步@newhar的评论学习,或者看@resolmi的链接 https://pasteme.cn/42461
public class Solution {
public static long[] pickApples(int[] a, int[] b) {
// 天数 苹果树数
int m = b.length, n = a.length;
long[] res = new long[m];
// 预排序
Arrays.sort(a);
int sum = 0;
// 指向苹果数的起点
int p = 0;
for (int i = 0; i < m; ++i) {
sum += b[i];
// 当天不够的树
while (p < n && a[p] < sum) {
// 这棵树减去前几天摘掉的果子,就是今天剩余的果子数
res[i] += a[p] - (sum - b[i]);
++p;
}
res[i] += (n - p) * b[i];
}
return res;
}
}
最后,希望能过二面吧,虽然廷凉的😥
