递归的原理及其机制
wecode
3342
2021.09.22
2022.06.05
发布于 未知归属地
C学习分享

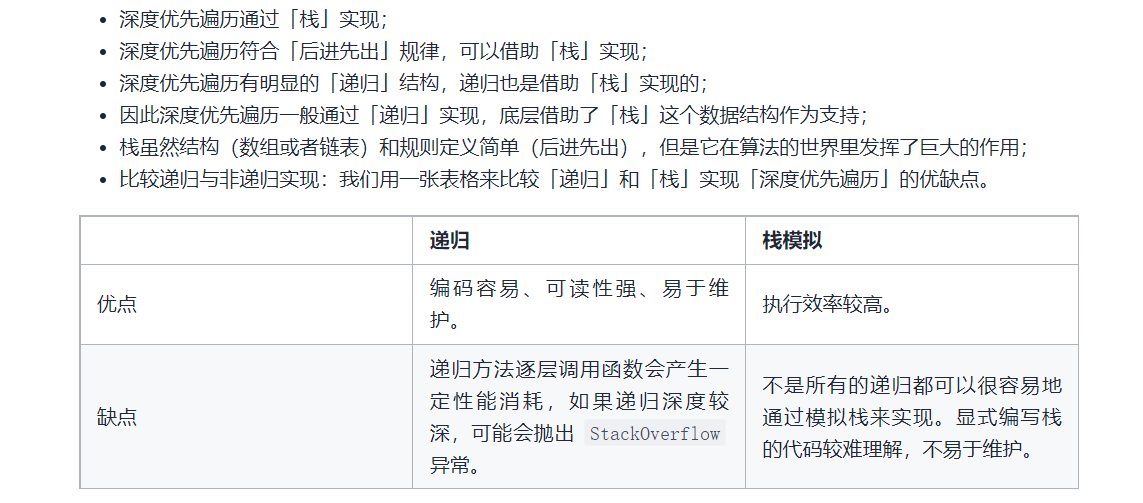
在回答递归函数怎么设计之前，我们先明确下递归函数的定义：函数进行自我调用，就被称为递归

你可能想知道一个函数怎样调用其自身。诀窍在于每次递归的调用其本身时，都将给定的问题缩小成其子问题，这样持续的递归调用，直到子问题可以不用递归就能解决的时候停止。

一个递归函数应该有以下属性：
1）具有简单的基本情况，即递归出口、递归结束条件，即不使用递归即可获得答案的情况；
(这样才不会导致无限循环)
2）一系列规则，称为recurrence relation递归关系，可以将问题逐步缩小直至递归出口；
注意，可能会有多个可以调用函数本身的地方。

为什么要引入递归的机制？

a) 因为计算机最擅长做重复的事情，递归机制实际是就是反复执行一段相同的逻辑代码。
函数的每个调用都代表给定任务的完整处理。

b) 如果执行一段相同的逻辑代码，直接用for或者while循环不行吗？为什么要用递归呢？
替代方案就是迭代算法，迭代算法就是for或者while循环语句，但递归算法因为更符合人类的思维方
式，更加简单有效，并且因为借助了系统栈（每个递归函数的所有局部变量，包括入参都会入堆栈），代码更加精简和可读。
主要原因还是代码精简，可读性好；

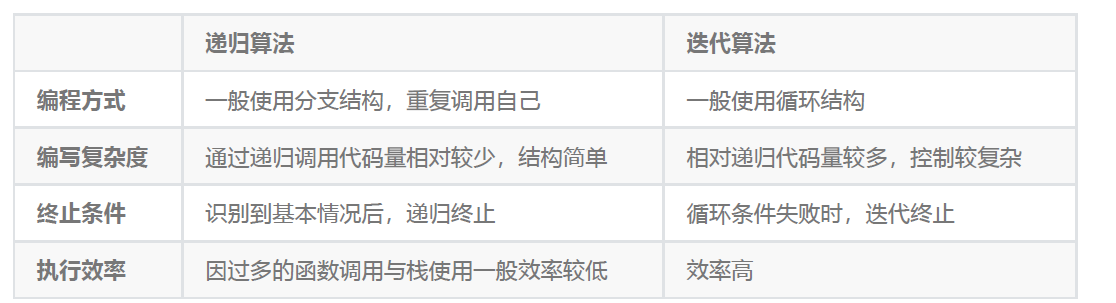
image.png

c) 递归机制的编程语言（目前几乎编程语言都支持），让程序员将精力都集中在递推关系逻辑的设计上，
简单说，就是充分利用编译器提供的好机制（编译器所产生的程序代码会应用栈的数据结构），解放程序员的一部分脑力；

d) 用递归写出来的代码可读性和可维护性都较好，它天然就是循环调用，但不用关心函数递归调用了多少次；
无需关心递归嵌套的深度，递归嵌套的执行用编程语言自动完成（程序员可以不关注）。

递归底层机制

关于递归函数调用，你需要知道的底层机制

https://lesley0416.github.io/2019/03/21/leetcode_explore_recursion/
https://blog.csdn.net/gegeyanxin/article/details/112118954?spm=1035.2023.3001.6557&utm_medium=distribute.pc_relevant_bbs_down.none-task-blog-2~all~first_rank_ecpm_v1~rank_v31_ecpm-2.nonecase&depth_1-utm_source=distribute.pc_relevant_bbs_down.none-task-blog-2~all~first_rank_ecpm_v1~rank_v31_ecpm-2.nonecase

为了完成一个典型的递归调用，系统需要分配一些空间来保存三部分重要的信息：

  1. 函数的返回地址：一旦函数调用完成，程序应该知道返回到哪里，即函数调用之前的位置；
  2. 函数传递的参数；
  3. 函数的局部变量；

为了说明这一点，以递归调用f(x1)→f(x2)→f(x3)为例，展示了执行步骤的顺序和堆栈布局。
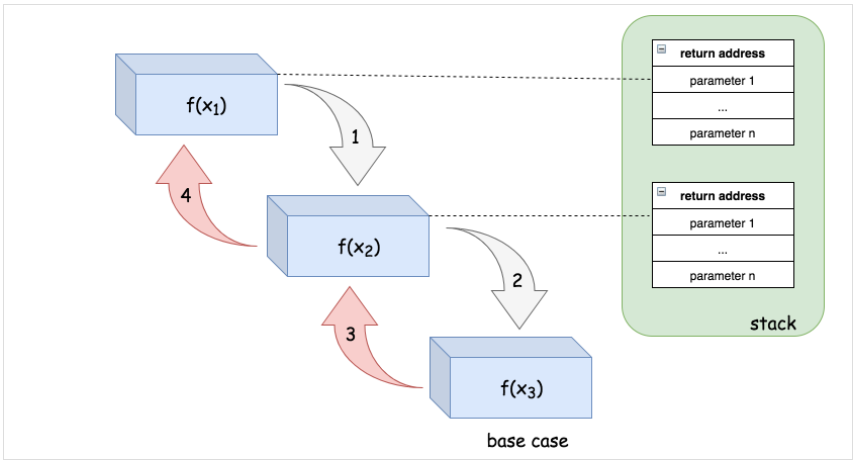
image.png

为了调用f(x2)，会给f(x1)分配一个栈空间。同理，在f(x2)中也会为了调用f(x3)而分配另一个栈空间。最终在f(x3)中，程序到达基本情况，因此没有在f(x3)中进一步递归。

由于这些递归相关的空间消耗，有时会导致栈溢出的情况，就是分配给一个程序的栈空间超出了其最大空间限制，导致程序失败。

因此，当设计递归算法时，一要仔细考虑当输入规模比较大的时候是否可能导致栈溢出；二来单层递归的局部变量也不宜过大。例如递归的深度为100个，单层递归的局部变量为10K，那么程序会消耗100 * 10K的堆栈空间；

a） 每次进行递归调用时，都会在栈中有自己的形参和局部变量的拷贝，这个由系统自动完成，即将所有的栈变量压入系统的堆栈；
b) 由于有了a)的机制，在递归返回的时候才能将前面压入栈的临时变量又恢复到现场；（注意恢复的是代码行级的现场，而不是函数级的现场，即不是说返回到原函数，又重新执行一遍）；
c) 递归函数的执行顺序较普通的函数不一样；

例如：
image.png

void dfs(int *nums, int depth, int *path, bool *used) 
{
    if (/*递归的出口*/) {
        return;
    }

    for (int i = 0; i < g_numsSize; i++) {
        if (used[i] == true) {
            continue;
        }

        used[i] = true;
        path[depth] = nums[i];
        dfs(nums, depth + 1, path, used);
        used[i] = false;
    }
}

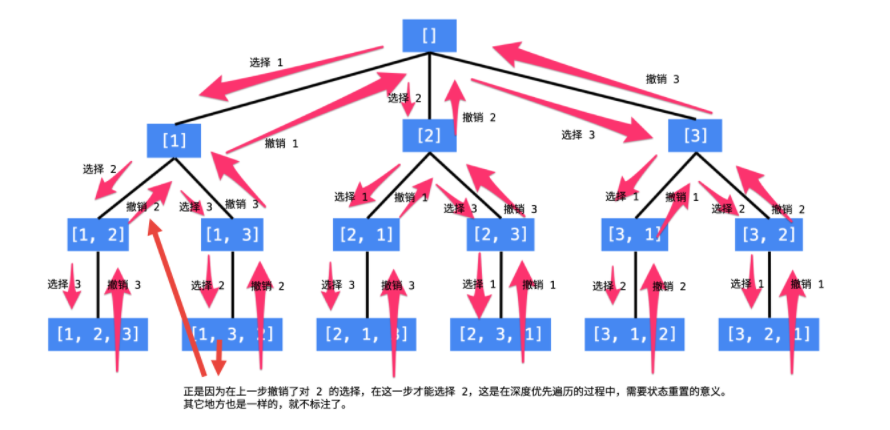
上面代码计算机执行的时候，我们很可能认为for循环的3次执行是齐头并进的（齐头并进的是广度优先遍历）

但实际上并不是这样的，而是以下面的方式执行Dfs0(nums, 0, path, used)
a) 执行Dfs(nums, 0, path, used)， (path为空列表，used全为false)。i=0， 需要执行used[0] = true; path[0] = 1; Dfs1(nums, 1, path, used); 碰到了递归函数，系统会将当前系统的i，depth局部变量，步骤a）的返回地址全部压入堆栈，执行Dfs(nums, 1, path, used)(path列表为1，used列表为true，false，false)；

b）执行Dfs(nums, 1, path, used)(path列表为1，used列表为true，false，false)。i = 0，跳过，i= 1，
执行used[1]= true, path[1] = 2; 再次碰到了递归函数，系统会将当前系统的i，depth局部变量，步骤b的返回地址全部压入堆栈，执行Dfs(nums, 2, path, used)(path列表为1，2，used列表为true，true，false)；

c) 执行Dfs(nums, 2, path, used)(path列表为1，2，used列表为true，true，false)。i=0跳过，i=1跳过，i=2，执行used[2]= true, path[2] = 3；再次碰到了递归函数，系统会将当前系统的i，depth局部变量, 步骤c)的返回地址全部压入堆栈，执行Dfs(nums, 3, path, used)(path列表为1，2, 3，used列表为true，true，true;

d）执行Dfs(nums, 3, path, used)(path列表为1，2, 3，used列表为true，true，true，满足递归的出口，输出结果【1,2,3】直接返回；执行完之后，跳转到c）中，恢复i=2，恢复depth=2，继续执行used[2] = false（回溯），for循环结束，c）中执行完毕；跳转到b）;

e）跳转到b）, 恢复i = 1，恢复depth=1，当前path列表为1,2,3，used列表为true，true，false，执行used[1]=false，used列表调整为true，false，false（回溯）; 进入i = 2，used[2]=true, path[1]=3; 碰到递归函数，系统会将当前系统的i，depth局部变量, 步骤e的返回地址全部压入堆栈，执行Dfs(nums, 2, path, used)(path列表为1，3，used列表为true，false，true);

f) 执行Dfs(nums, 2, path, used)(path列表为1，3，used列表为true，false，true), i=0跳过，i=1执行，执行used[1]=true, path[2]=2；碰到递归函数，系统会将当前系统的i，depth局部变量，步骤f的返回地址全部压入堆栈，执行Dfs(nums, 3, path, used)(path列表为1，3, 2，used列表为true，true，true);

g）执行Dfs(nums, 3, path, used)(path列表为1，2, 3，used列表为true，true，true)，满足递归的出口，输出结果【1,3,2】直接返回；执行完之后，跳转到f）；恢复i=1, depth=2, path列表为1，3,2，used列表为true，true，true; 执行used[1]=false（回溯）; 下一轮i=2, 结束循环，f)执行完毕；

h) 取出堆栈的栈顶地址，跳转到步骤e，恢复i=2，depth=1，used列表为true，false，true，执行used[2]=false（回溯）; 步骤e执行完毕；跳转到步骤a；恢复i=0，depth=0，path列表为1，used列表为true，false，false，执行used[0]=false（回溯）; i=1, used[1]=true, path[0]=2; 碰到递归函数，系统会将当前系统的i，depth局部变量, 步骤h的返回地址全部压入堆栈，执行Dfs(nums, 1, path, used)(path列表为2，used列表为false，true，false);

i) 执行Dfs(nums, 1, path, used)(path列表为2，used列表为false，true，false); i = 0，used[0]=true,path[1]=1; 再次碰到递归函数，系统会将当前系统的i，depth局部变量, 步骤i的返回地址全部压入堆栈，执行Dfs(nums, 2, path, used)(path列表为2,1，used列表为true，true，false);

j）.....

如果没有回溯过程，那么程序的执行如下：
a) 执行Dfs(nums, 0, path, used)， (path为空列表，used全为false)。i=0， 需要执行used[0] = true; path[0] = 1; Dfs1(nums, 1, path, used); 碰到了递归函数，系统会将当前系统的i，used, path，depth局部变量，步骤a）的返回地址全部压入堆栈，执行Dfs(nums, 1, path, used)(path列表为1，used列表为true，false，false)；

b）执行Dfs(nums, 1, path, used)(path列表为1，used列表为true，false，false)。i = 0，跳过，i= 1，
执行used[1]= true, path[1] = 2; 再次碰到了递归函数，系统会将当前系统的i，used, path，depth局部变量，步骤b的返回地址全部压入堆栈，执行Dfs(nums, 2, path, used)(path列表为1，2，used列表为true，true，false)；

c) 执行Dfs(nums, 2, path, used)(path列表为1，2，used列表为true，true，false)。i=0跳过，i=1跳过，i=2，执行used[2]= true, path[2] = 3；再次碰到了递归函数，系统会将当前系统的i，used, path，depth局部变量, 步骤c)的返回地址全部压入堆栈，执行Dfs(nums, 3, path, used)(path列表为1，2, 3，used列表为true，true，true);

d）执行Dfs(nums, 3, path, used)(path列表为1，2, 3，used列表为true，true，true)，满足递归的出口，输出结果【1,2,3】直接返回；执行完之后，跳转到c）中，恢复i=2，恢复depth=2，**不执行used[2] = false（不撤销对3的选择）**for循环结束，c）中执行完毕；跳转到b）;

e）跳转到b）, 恢复i = 1，恢复depth=1，不执行used[1]=false(不撤销对2的选择)，used列表仍然为true，true，true; 进入i = 2，不能选择任何元素，直接返回;

递归和深度优先遍历之间的关系：

image.png

评论 (2)