分享｜新手刷题第一步：先学好数据结构

61335

2024.08.29

2024.10.22

发布于广东

初来Leetcode刷题的小伙伴在还没有熟练掌握数据结构的使用和对底层原理的理解时，往往刷题会事倍功半。算法作为面试中非常核心的一环，攻克其高效的方法为先熟练掌握数据结构，再系统学习算法。本文会详细介绍面试中经常用到的数据结构数组，字符串，链表，哈希表，栈，队列，堆，优先队列，树，以及图的使用、底层原理以及各个操作的性能分析。

数组

一、数组的基本概念
数组是一种基本的数据结构，用于存储一系列固定大小的元素，这些元素类型相同。在数组中，每个元素都有一个对应的索引（或下标），通常从0开始，用于唯一标识数组中的每个位置。这种数据结构允许快速访问任何元素，因为通过索引，可以直接计算出元素的存储地址。

以下是数组在内存中的结构示意图和数组的索引示意图
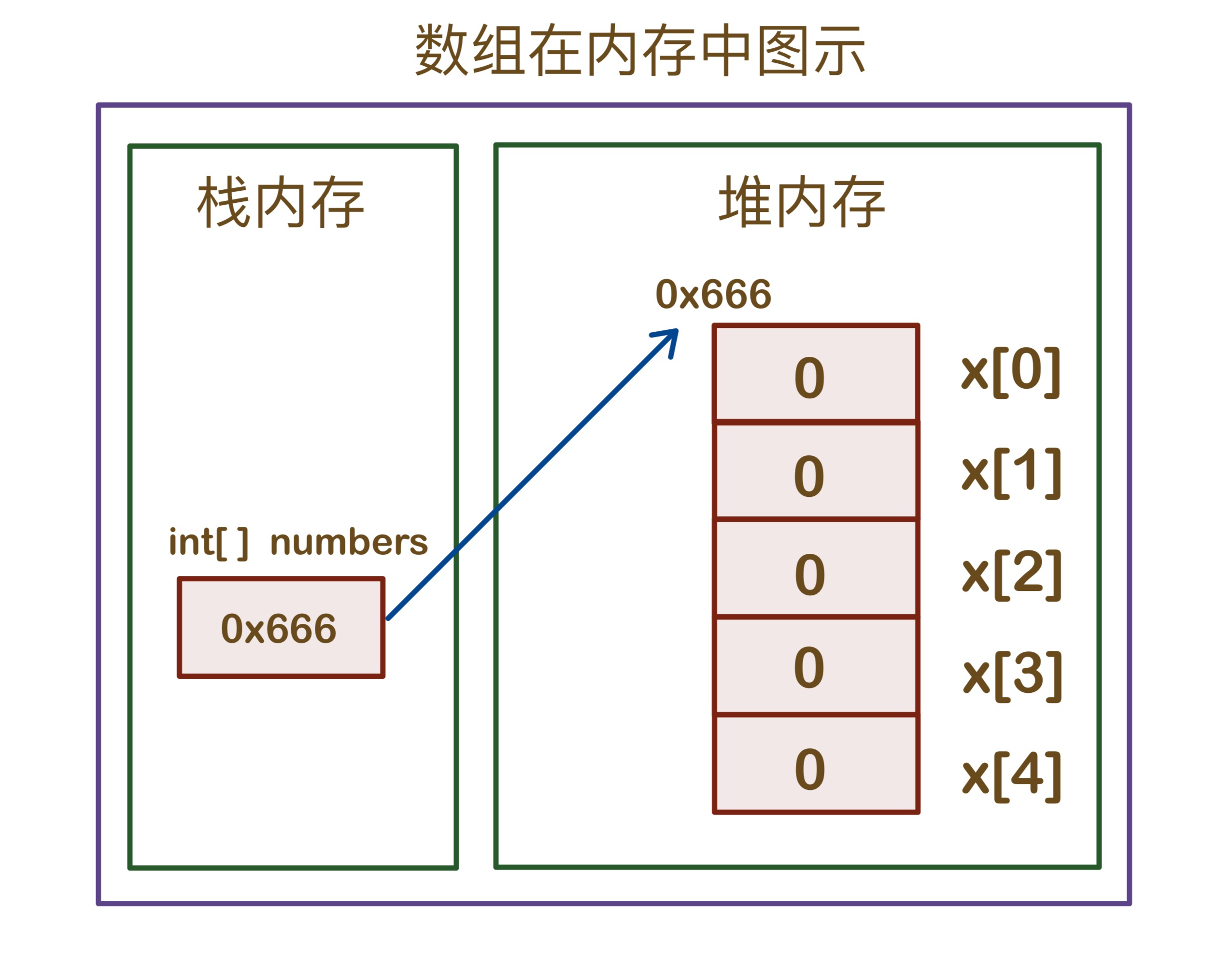
数组内存.jpg
数组索引.jpg

数组在内存中的存储方式是连续的，这是数组能够高效进行元素访问的关键原因之一。以下是数组在内存中存储的一些基本特性：

连续的内存空间：数组中的所有元素都存储在一块连续的内存区域。这意味着，如果你知道数组的起始地址（即第一个元素的地址），就可以通过简单的算术运算找到数组中任何元素的地址。
固定的元素大小：由于数组中的所有元素类型相同，它们的大小也是固定的。这使得通过索引来计算元素位置变得非常直接和高效。例如，如果数组的起始地址是 base_address，每个元素的大小是 element_size 字节，要访问索引为 i 的元素，该元素的内存地址就是 base_address + (i * element_size)。
索引访问：正是因为元素存储的连续性和大小的一致性，数组可以实现快速的随机访问。即访问任何一个元素的时间复杂度都是O(1)，这种访问速度不会随着数组大小的增加而变慢。
空间效率：数组由于其紧凑的存储方式，在空间使用上相当高效，不需要为存储元素间的关系或位置信息额外占用内存空间。但这也意味着数组的大小在创建时需要确定，并且在其生命周期内不可改变（不考虑动态数组或类似结构）。
内存分配方式：在静态数组的情况下，内存通常在编译时分配。而动态数组（如C++中的std::vector或Java中的ArrayList）允许在运行时动态改变大小，内存分配发生在堆上，可以动态增长或缩减，但仍保持元素的连续存储特性。
连续的内存存储模式使得数组在执行迭代访问和进行算术运算以定位元素时非常高效，但也限制了其大小的灵活性，这是在使用数组时需要考虑的一个重要因素。

1.数组的定义：
1.1 在 Java 中，创建一个数组通常包括以下几个步骤：

确定数组的数据类型。
声明数组的名称。
指定数组的长度。
初始化数组的元素。

1.2 数组在Java中可以通过以下几种方式创建：

使用数组变量声明和初始化数组：

public class Main {
    public static void main(String[] args){
        //声明一个整型数组变量；
        //int 表示整数类型；int[] 表示整数数组；numbers 表示整形数组名称
        int[] numbers; // 此时的numbers 只是一个引用变量，数组本身并不存在

        // 初始化数组numbers，即在内存中开辟一段连续的存储空间来存储5个整数
        // 所有元素的默认初始化值为0
        numbers = new int[5];
    }
}

//或者将声明和初始化合并到一起：

int[] numbers = new int[5];

直接声明并初始化数组：在声明数组的同时给数组赋初值，不需要指定数组的大小，编译器会根据提供的初始值自动确定数组的长度。

public class Main {
    public static void main(String[] args) {
        // 直接声明并初始化一个整型数组
        int[] numbers = {1, 2, 3, 4, 5};
    }
}

声明数组并分步初始化数组：先声明数组变量，然后在后续代码中为数组分配内存空间并逐个赋值。

public class Main {
    public static void main(String[] args){
        // 声明一个整型数组变量
        int[] numbers;

        // 在后续代码中为数组分配内存空间并赋初值
        numbers = new int[5];
        numbers[0] = 1;
        numbers[1] = 2;
        numbers[2] = 3;
        numbers[3] = 4;
        numbers[4] = 5;
    }
}

使用静态初始化块初始化数组：在类中使用静态初始化块为数组进行初始化。

// 声明数组并在静态初始化块中初始化
int[] numbers;

{
    numbers = new int[]{1, 2, 3, 4, 5};
}

1.3 拓展：二维数组的声明与创建

二维数组图示：
使用数组变量声明和创建数组：

public class Main {

    public static void main(String[] args){
        // 声明一个二维整型数组
        int[][] numbers;

        // 创建一个3行4列的二维数组，所有元素的默认初始化值为0
        numbers = new int[3][4];
        
        // 访问第一行第二列的元素: 0，并将其赋值于整数a
        int a = numbers[0][1];
    }
}

直接声明并初始化数组：在声明数组的同时给数组赋初值，不需要指定数组的大小，编译器会根据提供的初始值自动确定数组的长度。

public class Main {

    public static void main(String[] args){
        // 直接声明并初始化一个二维整型数组
        int[][] numbers = {
                {1, 2, 3, 4},
                {5, 6, 7, 8},
                {9, 10, 11, 12}
        };
    }
}

  学习了数组的定义之后，我们执行一维数据声明的代码，这时系统已经为数组分配了 5 个 int 类型的内存空间，如果我们想要能够对数组实现一些基本的功能，比如增删改查，那么我们可以自己来定义一个更完备的动态数组

2. 动态数组的实现
2.1这里我们定义了三个成员变量：
1. int[] 类型的 array 来表示数组
2. int 类型的 size 来计算数组的大小
3. int 类型的 num 来计算数组的里面的元素个数

2.2 构建一个有参构造函数，我们可以指定数组的大小，元素个数默认是 0 
2.3 再构建一个无参构造函数，默认大小为 10 ，元素个数默认是 0 
2.4 然后是一些相关的操作

public class MyArray {
    private int[] array;
    private int size;
    private int num;

    public MyArray(int size) {
        array = new int[size];
        this.size = size;
        num = 0;
    }

    public MyArray() {
        array = new int[10];
        size = 10;
        num = 0;
    }

    //加入元素
    public void add(int value) {
        ......
    }

    //获取元素
    public int get(int index) {
        ......
    }

    //删除元素
    public boolean delete(int x) {
        ......
    }

    //判断是否为空
    public boolean isEmpty() {
        ......
    }

}

二、数组的基本操作

基础操作在 Java 中的实现：
1.1 加入元素

就是在数组中放入元素，如下图示，在元素加入数组前，我们需要先判断数组中是否已满，而判断数组是否已满的条件就是，我们定义的数组中元素的个数跟数组的容量的比较（即数值相等），若相等，则数组已满，便没办法加入元素，需要先扩容。若数组没满，我们在原先计算元素个数的位置（可以理解为尾指针）放入元素，然后让元素个数 + 1

以下是运用数组实现数组加入元素的代码：

//加入元素
public void add(int value) {
    if (num == size) {
        // 数组扩容
        size = 2 * size;
        tempArray = array;
        array = new int[size];
        for (int i = 0; i < num; i++) {
            array[i] = tempArray[i];
        }
    }
    array[num++] = value;
}

1.2 获取元素

获取数组中指定的下标对应的某个元素，那么就需要传入 index ,然后将相应的元素返回
以下是运用数组实现获取元素的代码：

//获取元素
public int get(int index) {
    if (index < 0 || index >= num) {
        System.out.println("索引超出范围。");
        return -1;
    }
    
    return array[index];
}

1.3 判断数组是否为空

判断数组是否为空的条件是，我们定义的 num 是否为 0 ，因为我们最开始给 num 定义的初始值为 0 ，若未加入元素，num 是不会增加的，所以，当 num 的值仍为 0 时，说明数组未加入元素，那么数组为空
以下是运用数组判断数组是否为空的代码：

//判断是否为空
public boolean isEmpty() {
    return num == 0;
}

1.4 删除元素

在数组中删除指定的元素，如下图示，在数组删除元素之前，我们需要先判断数组中是否有元素，而判断数组是否为空的条件就是，我们定义的 num 是否为 0为，若 0 时，说明数组未加入元素，那么数组为空，返回 false ，若数组有元素，那么我们需要先定义一个索引 index 来记录在数组中搜索到的指定元素对应的下标。当 index 不为 -1 且 index 小于等于数组的大小时，证明我们找到了这个元素，那么就让这个元素后面的元素向前移动，然后让 num -1，返回 true ；若未找到元素，那么返回 false

以下是运用数组实现数组删除元素的代码：

//删除元素
public boolean delete(int x) {
    if (isEmpty()) {
        System.out.println("数组中没有元素");
        return false;
    }
    int index = -1;
    for (int i = 0; i < num; i++){
        if (x == array[i]) {
            index = i;
            break;
        }
    }
    if（index == -1）{
        return false;
    }
    for (int i = index; i < num - 1; i++){
        array[i] = array[i + 1];
    }
    num--;
    return true;
}

三、数组性能分析
数组是一种运用连续内存存储数据的数据结构，通过索引访问元素。

时间复杂度：
数组的随机访问效率高，按索引查找元素的时间复杂度为 O(1) ，但插入和删除操作效率较低，因为需要移动元素，时间复杂度为 O(n) ，其中 n 是数组中元素的个数。
空间复杂度：
因为数组需要连续的内存空间来存储元素，数组的空间复杂度为 O(n) ，其中 n 是数组的长度
适用场景：
元素数量固定、需要频繁随机访问元素的场景。
优点：
a. 随机访问效率高：数组的元素在内存中是连续存储的，因此可以通过索引直接访问任何元素
b. 无额外空间开销：数组的元素是连续存储的，数组本身在内存中的存储也是连续的，则数组在内存中占用的空间是紧凑的，没有额外的空间开销。
c. 易于实现和使用：数组是一种简单而直观的数据结构，在编程中易于实现和使用。
缺点：
a. 大小难改变：数组在创建时需要指定大小，且大小固定不可变，无法动态调整大小。如果数组的大小不足或者过大，都会导致资源的浪费或者无法满足需求。
b. 插入和删除效率低：在数组中插入或删除元素涉及到元素的移动，插入和删除操作的效率较低。
c. 需要连续内存空间：数组需要连续的内存空间来存储整个数组。如果没有足够的连续内存空间，可能会导致内存分配失败或者性能下降。

四、数组案例分析
1.两数之和

题目 Leetcode 链接：两数之和
例子：nums = [2, 7, 11, 15], target = 9
解题思路：在这道题，我们用一个 map 来存储，第一次，计算出 temp = 7，此时 map 中没有任何数据，所以把 2 0 放入 map 中，接着，i = 1，计算出 temp = 2 ，在 map 中搜索到 2 ，于是，答案数组为 0 1
相关题解：

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int[] res = new int[2];
        if(nums==null || nums.length==0){
            return res;
        }
        
        Map<Integer, Integer> map = new HashMap<>();
        for(int i=0; i<nums.length; i++) {
            int temp = target - nums[i];
            if(map.containsKey(temp)) {
                res[1] = i;
                res[0] = map.get(temp);
                break;
            }
            map.put(nums[i],i);
        }
        
        return res;
    }
}

2.移除元素

题目 leetcode 链接：移除元素
例子：nums = [3, 2, 2, 3], val = 3
解题思路：在这道题，我们用快慢指针，遍历数组，当遇到不是目标元素时，让慢指针指向的位置的元素变为快指针指向的元素。

移除元素2.jpg

相关题解：

class Solution {
    public int removeElement(int[] nums, int val) {
      int slow = 0;
        for(int fast = 0;fast<nums.length;fast++) {
            if(nums[fast]!=val){
                nums[slow++] = nums[fast];
            }
        }
        return slow;
     }
}

leetcode题单：数组知识点题库 - 力扣（LeetCode）

字符串

一、字符串的基本概念
字符串，是由 0 个或多个字符组合而成的有限序列，用于表示文本信息。在计算机科学中，字符串是一种基本的数据类型之一，通常用于存储和处理文本数据。
1.基本术语：

索引（下标）：索引是字符串中每个字符的唯一标识符，从 0 开始，依次递增。
字符：字符串由 0 个或多个字符组合而成，字符可以是数字、字母、标点符号等
长度：字符串中字符的个数
子串：字符串中截取连续的字符序列
空串：长度为 0 的串，注意，只有空格的串也不叫空串
在 Java 中，String 类型的值是不能修改的。

2.定义：
2.1 在 Java 中，字符串可以通过字符串字面值或使用构造函数来定义
2.2 字符串在 Java 中可以通过以下几种方式声明：
1. 使用构造函数

public class Main {
    public static void main(String[] args){
   
        String s1 = new String("hello");
    }
}

2. 直接赋值

public class Main {
    public static void main(String[] args){
   
        String s1 = "hello";
    }
}

2.3 字符串的基本方法在 Java 中的实现
2.3.1 Java 中由内置的引用类型：String

public class MyString {
    public static void main(String args[]) {
        String s1 = new String("hello");
        String s2 = new String("DataStruct");

        //连接两个字符串
        ......

        //输出字符串的长度
        ......

        //比较两个字符串
        ......    

        //输出字符串中的指定索引对应的字符
        ......

        //截取子串
        ......
                
    }
}

二、字符串的基本操作

基础操作在 Java 中的实现：
1.1 连接两个字符串

用 + 号连接即可
以下是连接两个字符串的代码：

//连接两个字符串
System.out.println(s1 + s2);

1.2 输出字符串的长度
以下是输出字符串的长度的代码：

//输出字符串的长度
System.out.println(s1.length());

1.3 比较两个字符串

用内置的 equals 函数比较
以下是比较两个字符串的代码：

//比较两个字符串
System.out.println(s1.equals(s2));

1.4 输出字符串中的指定索引对应的字符
以下是输出字符串中的指定索引对应的字符的代码：

//输出字符串中的指定索引对应的字符
System.out.println(s1.charAt(2));

1.5 截取子串
在 Java 中可以使用以下几种方法截取字符串中的子串：

使用substring方法

a. substring(int beginIndex)：从指定的索引beginIndex开始截取到字符串末尾。
例如：

     String str = "Hello World";
     String subStr = str.substring(6);
     System.out.println(subStr); // 输出 "World"

b. substring(int beginIndex, int endIndex)：从beginIndex开始（包括该索引处的字符），到endIndex结束（不包括该索引处的字符）截取子串。
例如：

     String str = "Hello World";
     String subStr = str.substring(0, 5);
     System.out.println(subStr); // 输出 "Hello"

使用split方法结合索引获取子串（适用于根据特定分隔符截取部分内容）
例如，从一个以逗号分隔的字符串中截取第二个子串：

    String str = "apple,banana,orange";
    String[] parts = str.split(","); // parts = ["apple", "banana", "orange"]
    if (parts.length > 1) {
        String subStr = parts[1];
        System.out.println(subStr); // 输出 "banana"
    }

使用charAt和循环手动构建子串（比较复杂的场景下）
例如，从一个字符串中每隔两个字符截取一个子串：

   String str = "abcdefghij";
   StringBuilder subStrBuilder = new StringBuilder();
   for (int i = 0; i < str.length(); i += 2) {
       subStrBuilder.append(str.charAt(i));
   }
   String subStr = subStrBuilder.toString();
   System.out.println(subStr); // 输出 "acegi"

三、字符串的模式匹配算法

BF 算法：
1.1 基础概念：
BF 算法是一种字符串匹配算法，也被称为朴素匹配算法。它从主串的每个位置开始，逐个比较主串和模式串的字符，找到匹配的位置。
1.2 核心思想：
遍历主串的每个位置，然后在该位置开始与模式串逐个字符比较。如果字符匹配成功，就继续比较下一个字符；如果字符不匹配，则从第一个匹配的 i + 1 开始，然后 j 从 1 开始重新比较。
1.3 时间复杂度：
O(nm)，其中 n 是主串的长度， m 是模式串的长度。在最坏情况下，需要比较 n * m 次。
1.4 Java 代码：

public static int bruteForceMatch(String host, String child) {
    int n = host.length();
    int m = child.length();

    for (int i = 0; i <= n - m; i++) {
        int j;
        for (j = 0; j < m; j++) {
            if (host.charAt(i + j) != child.charAt(j)) {
                break;
            }
        }
        if (j == m) {
            return i;
        }
    }
    return -1;
}

KMP 算法：
2.1 基础概念：
KMP算法避免在主串中进行不必要的回溯，提高字符串匹配的效率。运用这个算法前，我们需要先计算出 next j ,因为 KMP 算法它是主串和模式串无法匹配时，并不移动指向主串的 i ,而是移动指向模式串的 j ，而 next j 就是指向模式串的 j 匹配不成功的下一个移动位置。
2.2 核心思想：
构建一个部分匹配表，也就是 next j 用于存储模式串中每个位置对应的最长公共前后缀的长度。
2.3 时间复杂度：
O(n+m)，其中n是主串的长度，m是模式串的长度。在最坏情况下，只需要进行n次比较。
2.4 注意：
在这个代码中，计算 next j 的方法跟我们书本上学的计算方法有所不同，下面的代码用的是计算最大公共元素的长度，比如常规方法计算 ABAB 的 next j = {0, 1, 1, 2},而下面代码计算出来的 next j = {0, 0, 1, 2};
2.5 Java 代码：

public static int kmpMatch(String host, String child) {
    int n = host.length();
    int m = child.length();
    int[] next = computeNext(child);

    int i = 0, j = 0;
    while (i < n) {
        if (host.charAt(i) == child.charAt(j)) {
            i++;
            j++;
            if (j == m) {
                return i - j;
            }
        } else {
            if (j != 0) {
                j = next[j - 1];
            } else {
                i++;
            }
        }
    }
    return -1;
}

private static int[] computeNext(String child) {
    int m = child.length();
    int[] next = new int[m];
    int len = 0;
    int i = 1;

    while (i < m) {
        if (child.charAt(i) == child.charAt(len)) {
            len++;
            next[i] = len;
            i++;
        } else {
            if (len != 0) {
                len = next[len - 1];
            } else {
                next[i] = 0;
                i++;
            }
        }
    }
    return next;
}

四、字符串的性能分析
串是一种不可变的数据结构，它并不能在原地就进行修改操作。

时间复杂度：
字符串的常见操作（如获取长度等）的时间复杂度通常是 O(n) ，其中 n 是字符串的长度。
空间复杂度：
由于字符串（String）的不可变性，对字符串的操作可能会产生额外的空间开销，一般情况下，字符串的空间复杂度是 O(n) ，其中 n 是字符串的长度。
适用场景：
不能修改，但需要对数据进行处理和操作的场景。
优点：
a. 内容不可变：串是一种不可变的数据类型，增强了数据的安全性
b. 易于实现和使用：串是提供许多种方法的数据结构，使得对文本数据的处理变得简单和方便。
缺点：
a. 内容不可变：串是一种不可变的数据类型，一旦创建后内容不可修改，若需要频繁修改内容，则可能会产生大量的临时对象，增加了垃圾回收的压力和内存开销。
b. 插入和删除效率低：在串中插入或删除元素涉及到元素的移动，插入和删除操作的效率较低。
c. 内存空间开销大：当串较长时会占用大量的内存空间，可能会导致内存消耗较大。

五、字符串的案例分析
1.找出字符串中第一个匹配项的下标

题目链接：找出字符串中第一个匹配项的下标
例子：haystack = "sadbutsad", needle = "sad"
解题思路：在这道题中，我们用的是暴力匹配算法，当匹配不成功时，指向主串的指针往前移动一步，指向匹配串的指针从头开始。
相关题解：

class Solution {
    public int strStr(String haystack, String needle) {
        for (int i = 0 ;i <= haystack.length() - needle.length();i ++) {
            int j;
            for (j = 0;j < needle.length();j ++) {
                if (haystack.charAt(i + j) != needle.charAt(j)) {
                    break;
                }
            }
            if (j == needle.length()) {
                return i;
            }
        }
        return -1;
    }
}

2.字符串中的单词数

题目链接：字符串中的单词数
例子："Hello, my name is John"
解题思路：在这道题，我们用的目的就是找出前面一个是空格，并且它是个单词的连续串，那么我们就可以直接在循环中写出条件即可。
相关题解：

class Solution {
    public int countSegments(String s) {
        int res = 0;
        for (int i = 0;i < s.length();i ++) {
            if ((i == 0 || s.charAt(i - 1) == ' ') && s.charAt(i) != ' ') {
                res++;
            }
        }
        return res;
    }
}

leetcode题单：字符串知识点题库 - 力扣（LeetCode）

链表

一、链表的基本概念
链表是一种物理存储单元上不连续的存储结构。它由一系列节点组成，每个节点包含数据和一个指向下一个节点的引用。采用链式存储数据，解决了数组不方便移动，插入，删除元素的问题。

基本术语：

节点（ListNode）：链表的基本组成单元，包含数据域和指针域。
数据域（Data Field）：存储节点的实际数据。
指针域（Pointer Field）：存储指向下一个节点的引用。
头节点（Head ListNode）：链表的第一个节点，通常用于存储链表的起始位置。在一些实现中，头节点可能是一个哑节点（不存储有效数据），用于简化链表的操作。
尾节点（Tail ListNode）：链表的最后一个节点，其指针域通常为 null 或者 None，表示链表的终止。
哑节点（Dummy Node）/ 哨兵节点（Sentinel Node）：一个不存储有效数据的节点，通常作为链表的头节点或尾节点。用于简化链表的边界条件处理。
空链表（Empty List）：不包含任何节点的链表，头指针为 null。

链表1.jpg

链表2.jpg

链表3.jpg

2.链表的分类：

单链表
双链表
循环单链表

链表4.jpg

链表5.jpg

链表的定义
3.1 在 Java 中，链表可以通过节点类的定义和链表类的定义来声明。
3.2 这里我们首先定义一个结点类，这个结点类有两个成员变量：
1. int 类型的 data 来表示结点的数据
2. Node 类型的 next 来表示指向下一个结点的指针
3. 然后构造各种构造函数

3.3 构建一个链表类，这个结点类有三个成员变量：
1. Node 类型的 head 来表示头指针
2. Node 类型的 tail 来表示尾指针
3. int 类型的 size 来表示链表的大小
3.4 链表相关的操作

public class MyLinkedList {
    class ListNode{
        int val;
        ListNode next;
        
        //一个参数
        public ListNode(int val) {
            this.val = val;
        }

        //两个参数
        public ListNode(int val, ListNode next) {
            this.val = val;
            this.next = next;
        }

        //无参
        public Node() {
        }
    }
    class CustomList{
        ListNode head;
        ListNode tail;
        int size;

        public CustomList(ListNode head, ListNode tail, int size) {
            this.head = head;
            this.tail = tail;
            this.size = size;
        }

        public CustomList() {
    
        }
     }
     //1. 获取最末元素（ getLastNode() ），要求时间复杂度是O(1)

    public Node getLastNode() {
        ......
    }
    
    //2. 增加元素（ addNode(int value) ），要求时间复杂度是 O(1)

    public void addNode(int value) {
        ......
    }
    
    //3. 获取链表的长度（ getSize() ， return number of nodes ），要求时间复杂度是 O(1)

    public int getSize() {
        ......
    }
    
    //4. 展示链表元素
    public void display() {
        ......
}

二、链表的基本操作：

链表的基本操作：

链表的基本操作2.jpg

基础操作在 Java 中的实现：
2.1 获取最末元素（ getLastNode() ），要求时间复杂度是O(1)

就是在链表中获取元素，在此之前我们需要先判断尾指针是否为 null ，若它为 null，则证明链表中没有任何元素，返回 null ，若不为空，则将 tail 这个指针指向的 Node 返回
以下是链表获取最末元素的代码：
//1. 获取最末元素（ getLastNode() ），要求时间复杂度是O(1)

public Node getLastNode() {
    if (tail != null) {
        return tail;
    } else {
        System.out.println("此链表为空");
        return null;
    }
}

2.2 增加元素（ addNode(int value) ），要求时间复杂度是 O(1)

就是在链表中增加元素，首先我们将要加上的元素变为一个结点，然后判断尾指针是否为 null ，若它为 null，则证明链表中没有任何元素，那么就让头指针指向这个新结点，然后让尾指针也指向这个结点，若不为空，那么让尾指针指向的结点的下一个指向这个新节点，然后让尾指针再指向这个新节点。最后 size 要 + 1
以下是链表增加元素的代码：

//2. 增加元素（ addNode(int value) ），要求时间复杂度是 O(1)

public void addNode(int value) {
    ListNode NewNode = new ListNode(value);
    if (tail != null) {
        tail.next = NewNode;
    } else {
        head = NewNode;
    }
    tail = NewNode;
    size++;
}

2.3 获取链表的长度（ getSize() ， return number of nodes ），要求时间复杂度是 O(1)

在链表中，每次增加元素，都让 size ++，最后就能以 O(1) 的时间复杂度返回大小
以下是链表获取长度的代码：

//3. 获取链表的长度（ getSize() ， return number of nodes ），要求时间复杂度是 O(1)

public int getSize() {
    return size;
}

2.4 展示链表元素

在链表中，先判断头节点是否为空，若为空，此链表为空，若不为空，先建一个指针来遍历链表。
以下是链表展示元素的代码：

//4. 展示链表元素
public void display() {
    ListNode cur = head;
    if (head == null) {
        System.out.println("此链表为空");
    }
    while (cur != null) {
        System.out.print(cur.data + " ");
        cur = cur.next;
    }
    System.out.println();
}

三、链表的性能分析
链表是一种不是用连续内存存储数据的数据结构，通过指针连接结点。链表的插入和删除操作都只需要修改指针，因此时间复杂度为O(1)。然而，要获取特定位置的结点，需要遍历链表，时间复杂度为O(n)，这个和数组就有所区分。链表的常用方法包括插入结点(addNode)、获取最末元素（getLastNode）、获取链表长度（getSize）和遍历链表(display)。
四、链表的案例分析
1.合并两个有序链表

题目链接：合并两个有序链表
例子：l1 = [1,2,4], l2 = [1,3,4]
解题思路：在这道题，我们用两个指针，一个用于最后返回结果，一个用于遍历链表。遍历两个链表，当list1 的值小于等于 list2 时，让 cur 指针的下一个指向 list1 ，此时 list1 往下遍历它的下一个结点，cur 指向它自己的下一个结点。当 list1 的第二个结点大于 list2 第一个结点时，让 cur 的指针的下一个指向 list2，以此类推。最后，判断哪个链表已经到了最后，到了最后的话，就让 cur 的指针的下一个指向未到最后的那个。
相关题解：

class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        ListNode dummy = new ListNode(-1);
        ListNode cur = dummy;
        while (list1 != null && list2 != null) {
            if (list1.val <= list2.val) {
                cur.next = list1;
                list1 = list1.next;
            } else {
                cur.next = list2;
                list2 = list2.next;
            }
            cur = cur.next;
        }
        cur.next = list1 == null ? list2 : list1;
        return dummy.next;
    }
}

2.环形链表

题目链接：环形链表
例子：head = [3,2,0,-4], pos = 1
相关题解：这道题我们运用快慢指针，快指针一次走两步，慢指针一次走一步，当链表中存在环时，那么快慢指针会有重合，就返回 true ，否则返回 false
相关题解：

public class Solution {
    public boolean hasCycle(ListNode head) {
       if (head == null || head.next == null) {
            return false;
        }
        ListNode fast = head;
        ListNode slow = head;
        while (fast.next != null) {
            fast = fast.next;
            if (fast.next != null) {
                fast = fast.next;
            }
            if (fast == slow) {
                return true;
            }
            slow = slow.next;
        }
        return false;
    }
}

leetcode题单：链表知识点题库 - 力扣（LeetCode）

哈希表

一、哈希表的基本概念
哈希是一种使用哈希函数将键映射到值的数据结构。在计算机的应用中，如果我们想要实现字典，或者通过一个键搜索它对应的值，就需要用到哈希。它提供了快速的插入、删除和查找操作，适合用于需要高效查找的场景。

哈希表的定义：
哈希表（Hashtable，也叫散列表），是根据关键码值(Key value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中的某一个位置来访问值，存放值（记录）的数组叫做散列表。
哈希函数
a. 哈希表本质上也是一个数组
b. 哈希函数类似于一个中转站，把key和数组下标进行转换
c. 当发生哈希冲突时，即两个相同下标，但值不同的元素出现，我们需要使用开放寻址法或者链表法来解决。开放寻址法是“另谋高就”，就是直接寻找有空档的插入，不断往后移动，可以理解为 + 1 ；而链表法是通过一个链表，直接让 next 来指向下一个元素。

哈希表2.jpg

哈希表在 Java 中的定义
3.1 这里我们首先定义一个 HashEntry 类，这个 HashEntry 类有两个成员变量：
a. int 类型的 key 来表示键
b. String 类型的 value 来表示值
c. 并且要有 get 方法
3.2 构建一个 MyHashTable 类，这个 MyHashTable 类有两个成员变量：
a. int 类型的 TABLE_SIZE 来表示表的大小默认为 10 ，并且不能修改
b. HashEntry[] 类型的 myTable 来表示表，表中的每个元素都是键值对形式
c. 并且有一个构造函数，新建时给表的大小构建为 10
d. 再构建一个哈希函数，每次给加入的键分配位置

3.3 然后是一些相关的操作

public class MyHashTable {

    private class HashEntry {
        private int key;
        private String value;

        public HashEntry(int key, String value) {
            this.key = key;
            this.value = value;
        }

        public int getKey() {
            return key;
        }

        public String getValue() {
            return value;
        }
    }
    
    private static final int TABLE_SIZE = 10;
    private HashEntry[] myTable;

    public MyHashTable() {
        myTable = new HashEntry[TABLE_SIZE];
    }

    //加入键值对
    public void put(int key, String value) {
        ......
    }

    //按键查值
    public String get(int key) {
        ......
    }

    //删除键
    public void remove(int key) {
        ......
    }

    private int hashFunction(int key) {
        return key % TABLE_SIZE;
    }
}

二、哈希表的基本操作

基础操作在 Java 中的实现
1.1 给哈希表加入键值对
- 想要给哈希表加入键值对，我们就需要传入两个参数，一个是键一个是值，在进入之后调用哈希函数给键分配位置，倘若分配的位置已经有键了并且两个键不相同，那么就让 hash + 1 ，再重新给他分配个位置，直到可以放入为止。
  以下是给哈希表加入键值对的代码：

//加入键值对
public void put(int key, String value) {
    int hash = hashFunction(key);
    while (myTable[hash] != null && myTable[hash].getKey() != key) {
        hash = (hash + 1) % TABLE_SIZE;
    }
    myTable[hash] = new HashEntry(key, value);
}

1.2 在哈希表中按键查值
- 想要在哈希表中按键查值，我们就需要传一个参数键，在进入之后调用哈希函数找到键分配的位置，倘若分配的位置已经有键了并且两个键不相同，那么之前就产生过哈希冲突，那么就让 hash + 1 ，再重新找位置，直到找到为止，找到之后所对应的 hash 的值为空就返回空，否则就返回值
以下是在哈希表中按键查值的代码：

//按键查值
public String get(int key) {
    int hash = hashFunction(key);
    while (myTable[hash] != null && myTable[hash].getKey() != key) {
        hash = (hash + 1) % TABLE_SIZE;
    }
    if (myTable[hash] == null) {
        return null;
    } else {
        return myTable[hash].getValue();
    }
}

1.3 给哈希表删除键
- 想要给哈希表删除键，我们就需要传一个参数键，在进入之后调用哈希函数找到键分配的位置，倘若分配的位置已经有键了并且两个键不相同，那么之前就产生过哈希冲突，那么就让 hash + 1 ，再重新找位置，直到找到为止，找到之后若所对应的 hash 的值不为空就把它设置为空。
以下是在哈希表中按键查值的代码：

 //删除键
public void remove(int key) {
    int hash = hashFunction(key);
    while (myTable[hash] != null && myTable[hash].getKey() != key) {
        hash = (hash + 1) % TABLE_SIZE;
    }
    if (myTable[hash] != null) {
        myTable[hash] = null;
    }
}

注意：以上的实现没有写出哈希表满了之后的扩容机制，实际应用中可能需要根据具体情况进行调整和改进。
三、哈希表的性能分析
哈希表的性能主要取决于哈希函数的质量和哈希冲突的处理方式。一个好的哈希函数应该能够将不同的键尽可能均匀地映射到哈希表中，避免产生哈希冲突。在哈希表中，插入、删除和查找操作的时间复杂度通常是O(1)，但是，如果哈希函数不好、哈希冲突较多，则可能导致性能下降。
哈希表的性能分析是一个复杂的问题，因为它需要考虑数据、哈希函数、哈希冲突等多个因素。

四、哈希表的案例分析
3. 两数之和

题目链接：两数之和
例子：nums = [2,7,11,15], target = 9
解题思路：在这道题，我们用一个 map 来存储，第一次，计算出 temp = 7，此时 map 中没有任何数据，所以把 2 0 放入 map 中，接着，i = 1，计算出 temp = 2 ，在 map 中搜索到 2 ，于是，答案数组为 0 1
相关题解：

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int []res = new int[2];
        if(nums==null||nums.length==0){
            return res;
        }
        Map<Integer,Integer> map = new HashMap<>();
        for(int i=0;i<nums.length;i++) {
            int temp = target-nums[i];
            if(map.containsKey(temp)) {
                res[1] = i;
                res[0] = map.get(temp);
                break;
            }
            map.put(nums[i],i);
        }
        return res;
    }
}

4.四数相加 II

题目链接：四数相加 II
例子：nums1 = [1,2], nums2 = [-2,-1], nums3 = [-1,2], nums4 = [0,2]
解题思路：这道题是要我们能够找出 i j k l 并让它们对应的值能够加起来为 0 。这道题我们用到 map ，用 map 统计 i + j 的值，然后将它们的值作为键，次数为值存入 map 中，然后遍历后两个数组，用 0 去减它们 i 和 j 相加的值，得出的值如果在 map 中出现过，res 在此时就加上对应的次数，也就是键相对应的值。
相关题解：

class Solution {
     public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
        int res = 0;
        HashMap<Integer,Integer> map = new HashMap<>();
        for(int i:nums1){
            for(int j:nums2){
                int sum = i+j;
                map.put(sum,map.getOrDefault(sum,0)+1);
            }
        }
        for(int i:nums3){
            for(int j:nums4){
                res+=map.getOrDefault(0-i-j,0);
            }
        }
        return res;
    }
}

leetcode题单：哈希表知识点题库 - 力扣（LeetCode）

栈

一、栈的基本概念
在学习栈之前，我们首先要了解栈的本身的意思。在汉字中，它可以解释为存储货物的仓库或者是留宿客商的房屋。而在计算机之中，他就是暂时存储数据的地方，也可以理解为存储数据的仓库。
1.栈的定义：

栈（又名：堆栈）是一种只能在一段进行插入或删除操作的线性表（受限的线性表）
特点：先进后出
可以将栈想象成一个羽毛球筒，我们先放入的往往最后拿出来。

2.基础概念：

栈顶 (Top)：（进出口）表中允许进行插入或删除操作的一端
栈底 (Bottom):栈顶和栈底是相对而言的，一端被称作为栈顶，相对的，另一端就被称作为栈底。
空栈：栈中没有元素
满栈：栈中已放满元素
以下是图例

3.栈在 Java 中的定义
3.1 这里我们定义了三个成员变量：
1. int[] 类型的 stack 来表示栈
2. int 类型的 rear 来表示栈顶指针
3. int 类型的 size 来计算栈的大小
3.2 构建一个有参构造函数，我们可以指定栈的大小，而栈顶指针默认是 0 ，指向栈底
3.3 然后是一些相关的操作

public class MyStack {
    int[] stack;
    int rear;
    int size;

    public MyStack(int size) {
        stack = new int[size];
        rear = 0;
        this.size = size;
    }

    //入栈
    public void push(int value) {
        ......    
    }

    //出栈
    public int pop() {
        ......
    }

    //判断是否为空
    public boolean isEmpty() {
        ......
    }

    //查看栈顶元素
    public int peek() {
        ......
    }
}

二、栈的基本操作

顺序栈的基本操作：
基本操作在 Java 中的实现
2.1 入栈

入栈就是在栈中放入元素，在元素入栈前，我们需要先判断栈中是否已满，而判断栈是否已满的条件就是，我们定义的尾指针是否已经走到跟栈的容量一样的位置（即数值相等），若相等，则栈已满，便没办法加入元素，需要先扩容。若栈没满，我们在原先尾指针的位置放入元素，然后将尾指针向后移动。
因为我们此时是用数组实现的栈，因此，在栈中，我们可以将上文所指的尾指针看成栈顶指针。让栈顶指针移动到栈顶，即走的距离等于栈的容量大小时，栈已满。
以下是运用数组实现栈加入元素的代码：

//入栈
public void push(int value) {
    if (rear == size) {
        System.out.println("栈已满，需要扩容");
    }
    stack[rear++] = value;
}

2.2 出栈

出栈就是让栈中的元素弹出，在元素弹出栈前，我们需要先判断栈中是否还有元素，而判断栈是否为空的条件就是，我们定义的尾指针是否为 0 ，因为我们最开始给尾指针定义的初始值为 0 ，若未加入元素，尾指针是不会移动的，所以，当尾指针的值仍为 0 时，说明栈未加入元素，那么栈为空，就弹不出元素，返回 -1 ；若栈中有元素，那么我们将尾指针现在所指的元素返回，并让尾指针向前移动。
因为我们此时是用数组实现的栈，因此，在栈中，我们可以将上文所指的尾指针看成栈顶指针。当栈顶指针指向栈底，即 = 0 时，则栈为空；若栈不为空，弹出元素后，让栈顶指针向栈底方向移动。
以下是运用数组实现栈弹出元素的代码：

//出栈
public int pop() {
    if (isEmpty()) {
        System.out.println("栈中没有元素");
        return -1;
    }
    return stack[--rear];
}

2.3 判断栈是否为空

判断栈是否为空的条件是，我们定义的尾指针是否为 0 ，因为我们最开始给尾指针定义的初始值为 0 ，若未加入元素，尾指针是不会移动的，所以，当尾指针的值仍为 0 时，说明栈未加入元素，那么栈为空
以下是运用数组判断栈是否为空的代码：

//判断是否为空
public boolean isEmpty() {
    return rear == 0;
}

2.4 查看栈顶元素

查看栈顶元素之前，我们仍旧需要判断栈是否为空，判断之后，若栈中无元素，则返回 -1 ，若栈中有元素，则将当前尾指针（栈顶指针）所指的元素返回。
以下是运用数组查看栈顶元素的代码：

//查看栈顶元素
public int peek() {
    if (isEmpty()) {
        System.out.println("栈中没有元素");
        return -1;
    }
    return stack[rear - 1];
}

链栈的实现：
3.1 链栈的定义：栈的链式存储结构称为链栈。就是一种限制运算的链表，链表有栈的特性，即规定链表中的插入和删除运算只能在链表开头进行。
3.2 图示：

3.3 Java中实现（代码）：

public class LinkedStack {
    
    //定义一个对象来表示栈的每个结点
    public class Node {
        //一个存放数据一个存放指向下一个的指针
        private Object value;
        private Node next;

        public Node() {
        }

        public Node(Object value) {
            this.value = value;
            this.next = null;
        }

        public Node(Object value, Node next) {
            this.value = value;
            this.next = next;
        }
    }
    
    //栈顶指针
    private Node top;
    
    //入栈
    public void push(Object a) {
        top = new Node(a , top);
    }
    
    //出栈
    public boolean pop() {
        if (IsEmpty()) {
            System.out.println("栈中没有元素，空栈");
            return false;
        }
        top = top.next;
        return true;
    }
    
    //判断栈是否为空
    private boolean IsEmpty() {
        return top == null;
    }
    
    //获取栈顶元素
    public Object peek() {
        if (IsEmpty()) {
            System.out.println("栈中没有元素，空栈");
            return null;
        }
        return top.value;
    }
    
    //获取栈的长度
    public int getSize() {
        Node p = top;
        int size = 0;
        while (p != null) {
            p = p.next;
            size++;
        }
        return size;
    }
    
}

三、栈的性能分析
栈是一种后进先出(LIFO)的数据结构。在栈中，插入和删除操作都是发生在栈顶。由于栈的特性，插入和删除操作都只需要时间复杂度O(1)。栈的常用方法包括入栈(push)、出栈(pop)、查看栈顶元素(peek)、获取栈的长度（getSize）和判断栈是否为空(isEmpty)。

四、栈的案例分析
1.逆波兰表达式求值

题目链接：逆波兰表达式求值
例子：tokens = ["2","1","+","3","*"]
解题思路：在这道题，当我们遇见数字时，就将他入栈，如果遇到符号时，就将栈中的两个元素弹出，让他们进行符号需要的加减乘除运算，再将结果重新放入栈内。
相关题解：

public class Solution {
    public int evalRPN(String[] tokens) {
        Stack<Integer> stack = new Stack<>();
        for (String token : tokens) {
            if (Objects.equals(token, "+")) {
                stack.add(stack.pop() + stack.pop());
            } else if (Objects.equals(token, "-")) {
                int a = stack.pop();
                int b = stack.pop();
                stack.add(b - a);
            } else if (Objects.equals(token, "*")) {
                stack.add(stack.pop() * stack.pop());
            } else if (Objects.equals(token, "/")) {
                int a = stack.pop();
                int b = stack.pop();
                stack.add(b / a);
            } else {
                stack.add(Integer.valueOf(token));
            }
        }
        return stack.pop();
    }
}

2.括号的最大嵌套深度

题目链接：括号的最大嵌套深度
例子：s = "(1)+((2))+(((3)))"
解题思路：在这里，我们新建一个栈对象，当遇到 ' ( ' 这个符号时，就将他入栈，如果遇到 ' ) ' 这个符号，且这时候栈顶元素为 ' ( ' 时，则匹配到一个括号，那么就 res 就为当前栈的大小和 res 已有的值之间的最大值
相关题解：

class Solution {
    public int maxDepth(String s) {
        Stack<Character> stack = new Stack<>();
        int res = 0;
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == '('){
                stack.add(s.charAt(i));
            }
            if (s.charAt(i) == ')' && stack.peek() == '(') {
                res = Math.max(res,stack.size());
                stack.pop();
            }
        }
        return res;
    }
}

leetcode题单：栈知识点题库 - 力扣（LeetCode）

队列

一、队列的基本概念
在学习队列之前，我们首先要了解队列的本身的意思。在汉字中，它是人物、对象排成的直行和横列的总称，有整齐、有秩序等特点。那么在计算机中，有些数据我们需要先处理，但是因为已经有正在处理的数据，于是我们把它放进有队列的缓冲区，当我们处理完手头上的任务之后，我们就能按照先来后到的顺序来处理缓冲区里的任务。

1.队列的定义：

队列（Queue）是一种先进先出(FIFO, First-In-First-Out)的数据结构。
特点：先进先出（注意：这点与栈不同，队列是先进先出，可以想象成排队，而栈可以想象成一个羽毛球筒）
队列是一种只允许在一端进行插入操作，在另一端进行删除操作的先入先出的受限的线性表。

2.基础概念：

队头（Front）：允许删除的一端，又称队首
队尾（Rear）：允许插入的一端
空队列：不包含任何元素的空表
队满：队中已放满元素
以下是图示：

3.队列在 Java 中的定义

3.1 这里我们定义了五个成员变量：
1. int[] 类型的 queue 来表示队列
2. int 类型的 capacity 来表示队列的容量
3. int 类型的 front 来表示队列的头指针
4. int 类型的 rear 来表示队列的尾指针
5. int 类型的 size 来表示队列中元素的数量
3.2 构建一个有参构造函数，我们可以指定队列的最大容量，而队列的头指针默认为 0 ，尾指针默认是 -1 ，队列大小默认为 0
3.3 然后是一些相关的操作

public class MyQueue {
    private int[] queue;
    private int capacity;
    private int front;
    private int rear;
    private int size;

    public MyQueue(int capacity) {
        this.capacity = capacity;
        queue = new int[capacity];
        front = 0;
        rear = -1;
        size = 0;
    }
    
    //判断是否为空
    public boolean isEmpty() {
        ......
    }
    
    //判断是否已满
    public boolean isFull() {
        ......
    }

    //入队
    public void push(int value) {
        ......
    }

    //出队
    public int pop() {
        ......
    }

    //查看队头元素
    public int peek() {
        ......
    }

    //查看队列大小
    public int size() {
        ......
    }
}

二、队列的基本操作

顺序队列的基础操作：
基本操作在 Java 中的实现：
2.1 入队

入队就是在队列中放入元素，在元素入队前，我们需要先判断队列中是否已满，而判断队列是否已满的条件就是，我们定义的大小跟队列的最大容量的比较（即数值相等），若相等，则队列已满，便没办法加入元素，需要先扩容。若队列没满，我们在原先尾指针的位置放入元素，然后将尾指针向后移动，并且 size 要 + 1
rear = (rear + 1) % capacity 这里用这个是为了在循环队列中的运用。这里的 (rear + 1) 表示队尾指针后移一位，而 % capacity 则是为了将队尾指针限制在数组范围内。
以下是运用数组实现队列加入元素的代码：

//入队
public void push(int value) {
    if (isFull()) {
        System.out.println("队列已满，无法入队");
        return;
    }

    rear = (rear + 1) % capacity;
    queue[rear] = value;
    size++;
}

2.2 出队

出队就是让队列中的元素弹出，在元素弹出队列前，我们需要先判断队列中是否还有元素，而判断队列是否为空的条件就是，我们定义的 size 是否为 0 ，因为我们最开始给 size 定义的初始值为 0 ，若未加入元素，size 是不会增加的，所以，当 size 的值仍为 0 时，说明队列未加入元素，那么队列为空，就弹不出元素，返回 -1 ；若队列中有元素，那么情况就比较复杂，因为我们队列是先进先出的特点，所以我们需要将第一个元素先保存下来，然后让头指针向后移动，并让 size - 1
front = (front + 1) % capacity; 这里的 (front + 1) 表示队首指针后移一位，而 % capacity 则是为了将队首指针限制在数组范围内。
以下是运用数组实现栈弹出元素的代码：

//出队
public int pop() {
    if (isEmpty()) {
        System.out.println("队列为空，无法出队");
        return -1;
    }

    int temp = queue[front];
    front = (front + 1) % capacity;
    size--;

    return temp;
}

2.3 判断队列是否为空

判断队列是否为空的条件是，我们定义的 size 是否为 0 ，因为我们最开始给 size 定义的初始值为 0 ，若未加入元素，size 是不会增加的，所以，当 size 的值仍为 0 时，说明队列未加入元素，那么队列为空
以下是运用数组判断队列是否为空的代码：

//判断是否为空
public boolean isEmpty() {
    return size == 0;
}

2.4 判断队列是否已满

队列是否已满的条件是，我们定义的大小跟队列的最大容量的比较（即数值相等），若相等，则队列已满，便没办法加入元素
以下是运用数组判断队列是否已满的代码：

//判断是否已满
public boolean isFull() {
    return size == capacity;
}

2.5 查看队头元素

查看队头元素之前，我们仍旧需要判断队列是否为空，判断之后，若队列中无元素，则返回 -1 ，若队列中有元素，则将当前头指针所指的元素返回。
以下是运用数组查看队头元素的代码：

//查看栈顶元素
public int peek() {
    if (isEmpty()) {
        System.out.println("队列为空");
        return -1;
    }

    return queue[front];
}

2.6 查看队列的大小
以下是运用数组查看队列大小的代码：

//查看队列的大小
public int size() {
    return size;
}

双端队列
3.1 双端队列的定义：允许两头都能进入元素，两头都出去元素，这种队列叫双端队列，即Deque
3.2 图示：

三、队列性能分析
队列是一种先进先出(FIFO)的数据结构。在队列中，插入操作在队尾，删除操作在队首。跟栈类似，队列的插入和删除操作都只需要时间复杂度 O(1) 。队列的常用方法包括入队 (push) 、出队(pop) 、查看队首元素 (peek) 和判断队列是否为空 (isEmpty)等。
虽然队列的各种操作的时间和空间复杂度都是 O(1) ，但是在某些特殊情况下，比如当队列的大小超过了事先分配的内存空间时，可能就需要进行动态扩容操作，而这样的操作会导致入队操作的时间复杂度变为 O(n) ，其中 n 是当前队列的大小。因为这种情况出现的频率较低，所以平均情况下近似认为是O(1)的时间复杂度。

四、队列案例分析
1.用队列实现栈

题目链接：用队列实现栈
解题思路：在这道题，我们的任务是用队列实现栈，那么我们就是用队列实现先进后出，那么我们要做的就是，每次要弹出元素，就让队头的元素重新加入队尾，这样可以让第一个元素就是要弹出的元素恰好是最后面加入的元素。
相关题解：

class MyStack {
    Queue<Integer> queue;

    public MyStack() {
        queue = new LinkedList<>();
    }

    public void push(int a) {
        int n = queue.size();
        queue.offer(a);
        //让原先的先出队再入队
        for (int i = 0; i < n; i++) {
            queue.offer(queue.poll());
        }
    }

    public int pop() {
        return queue.poll();
    }

    public int top() {
        return queue.peek();
    }

    public boolean empty() {
        return queue.isEmpty();
    }
}

2.用栈实现队列

题目链接：用栈实现队列
解题思路：在这道题，我们的任务是用栈实现队列，那么我们就是用栈实现先进先出，那么我们需要用到两个栈，一个来存放入的元素，一个来存要弹出的元素。要弹出元素时，我们先判断弹出栈里面有没有元素，如果是空的，则将放入栈中的元素全都弹到弹出栈里面，然后再将弹出栈的第一个元素弹出，这样就完成一次反序。
相关题解：

class MyQueue {
    Stack<Integer> stackIn;
    Stack<Integer> stackOut;

    public MyQueue() {
        stackIn = new Stack<>();
        stackOut = new Stack<>();
    }

    public void push(int x) {
        stackIn.push(x);
    }

    public int pop() {
        if (stackOut.isEmpty()) {
            while (!stackIn.isEmpty()) {
                stackOut.push(stackIn.pop());
            }
        }
        return stackOut.pop();

    }

    public boolean empty() {
        return stackIn.isEmpty() && stackOut.isEmpty();
    }

    public int peek() {
        if (stackOut.isEmpty()) {
            while (!stackIn.isEmpty()) {
                stackOut.push(stackIn.pop());
            }
        }
        return stackOut.peek();
    }
}

leetcode题单：队列知识点题库 - 力扣（LeetCode）

树（主要讨论二叉树）

一、树的基本概念
在学习树之前，我们首先要了解树本身的意思。在汉字中，它是表示一种木本植物，由根、干、枝、叶、花、果组成。而在计算机中，它并没有这么复杂，只由根节点和子树组成，它被引申为一个集合和该集合定义的一些子集之间的关系。
1.树的定义：

树（Tree）是由 n (n >= 0 ) 个结点组合成的有限集合。
当 n = 0 时，说明这是一棵空树
若不是一棵空树，那么该树有且仅有一根节点
图示的是多叉树

2.基本术语

树的节点（node）：树中的数据元素
孩子节点（child node）：树中节点的左右节点
父节点：B 节点是 A 节点的孩子节点，则 A 节点是 B 节点的父节点
兄弟节点：是同一父节点的孩子节点
树的深度：从上往下数，节点的最大深度
树的高度：从下往上数，节点的最大高度。
节点的度：节点拥有的子树的个数
树的度：树中最大的节点度。
叶子节点：是度为 0 的节点，即没有子树的节点

3.二叉树的特点：

二叉树是每个节点最多有两个子树的树结构，这两个子树通常被称为左子树和右子树。每个节点可以有零个、一个或两个子节点。

4.二叉树的特殊类型

满二叉树：在一颗二叉树中，除了叶节点外，每个节点都有 2 个子节点。
完全二叉树：在一颗二叉树中，若除最后一层外的其余层都是满的，并且最后一层要么是满的，要么在右边缺少连续若干节点。以根节点深度为 1 计算，具有 n 个节点的完全二叉树的深度为 logn + 1。深度为 k 的完全二叉树，至少有2^(k - 1) 个节点，至多有 2^k - 1 个节点。
二叉搜索树：在一颗二叉树中，左子树的所有节点的值都小于根节点的值；右子树的所有节点的值都大于根节点的值。

5.二叉树的存储方式

链表存储：每个节点包含数据域、左指针域和右指针域，分别指向左子树和右子树。这种存储方式灵活，但占用空间相对较大，因为每个节点都需要额外的指针空间。
数组存储：对于完全二叉树，可以用数组来存储，利用数组的索引来表示节点之间的关系。如果一个节点的索引是 i，那么它的左子节点的索引是 2i + 1，右子节点的索引是 2i + 2。这种存储方式简单，但只适用于完全二叉树，对于一般的二叉树可能会浪费很多空间。

链式存储
顺序存储

6.二叉树在 Java 中的定义
6.1 这里我们首先定义一个节点类，这个节点类有三个成员变量：

int 类型的 val 来表示节点的数据
TreeNode 类型的 left 来表示指向左节点的指针
TreeNode 类型的 right 来表示指向右节点的指针
然后构造一个 val 的构造函数

6.2 构建一个树类，这个节点类有一个成员变量：
1. TreeNode 类型的 root 来表示根节点

6.3 常见的操作

import java.util.LinkedList;
import java.util.Queue;

public class BinaryTree {
    class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        public TreeNode(int val) {
            this.val = val;
        }
    }

    private TreeNode root;

    public BinaryTree(TreeNode root) {
        root = null;
    }

    //前序遍历
    public void preOrderTraversal(TreeNode root) {
        ......
    }

    //中序遍历
    public void inOrderTraversal(TreeNode root) {
        ......
    }

    //后序遍历
    public void postOrderTraversal(TreeNode root) {
        ......        
    }

    //层序遍历
    public void levelOrderTraversal(TreeNode root) {
        ......
    }

}

二叉树的遍历方式
二叉树主要有两种遍历方式：
1.深度优先遍历：持续往下走，当走到没有路径可走的节点时，便返回上一级节点继续探索其他路径。
1. 前序遍历（中左右）
2. 中序遍历（左中右）
3. 后序遍历（左右中）
  注意：前后序不能构建二叉树。

2.广度优先遍历：一层一层的去遍历
层序遍历：1 2 3 5 6 7 8

8.多叉树的性质特点：

多叉树中的节点可以有多个，它不止两个节点
多叉树的子树也是多叉树，可以递归地定义
多叉树的高度可能会比较小，因为它每个节点都可以有多个节点

9.多叉树的存储方式：比较多使用节点和指针来表示，可以参考二叉树的链式存储

10.二叉树与多叉树的异同点

相同点：
1. 都属树结构，都具有树的基本特质
2. 都可以表示层次关系
不同点：
1. 它们的子节点数量不同，二叉树每个节点最多有两个，而多叉树没有限制
2. 多叉树通常不会使用跟二叉树一样的顺序存储，即使用数组。

二、二叉树的基本操作:它们的时间复杂度和空间复杂度取决于树的结构和深度
1.基本操作：

前序遍历：
- 时间复杂度：O(n)（n为节点数）
- 空间复杂度：O(h)（h为树的高度）
- 当根节点不为 null 时，先访问根节点，再访问根节点的左子树，最后访问根节点的右子树

//前序遍历
public void preOrderTraversal(TreeNode root) {
    if (root == null) {
        return;
    }
    System.out.print(root.val + " ");
    preOrderTraversal(root.left);
    preOrderTraversal(root.right);
}

中序遍历：
- 时间复杂度：O(n)（n为节点数）
- 空间复杂度：O(h)（h为树的高度）
- 当根节点不为 null 时，先访问根节点的左子树，再访问根节点，最后访问根节点的右子树

//中序遍历
public void inOrderTraversal(TreeNode root) {
    if (root == null) {
        return;
    }
    inOrderTraversal(root.left);
    System.out.print(root.val + " ");
    inOrderTraversal(root.right);
}

后序遍历:
- 时间复杂度：O(n)（n为节点数）
- 空间复杂度：O(h)（h为树的高度）
- 当根节点不为 null 时，先访问根节点的左子树，再访问根节点的右子树，最后访问根节点

//后序遍历
public void postOrderTraversal(TreeNode root) {
    if (root == null) {
        return;
    }
    postOrderTraversal(root.left);
    postOrderTraversal(root.right);
    System.out.print(root.val + " ");
}

层序遍历：
- 时间复杂度：O(n)
- 空间复杂度：O(w)（w为树的最大宽度）
- 当根节点不为 null 时，把根节点放入队列，判断队列是否为空，当队列不为空时，将队列中的第一个元素输出，然后判断这个元素的左子树是否存在，存在就将其放入队列，再判断右子树是否存在，存在就将其放入队列。不断判断队列是否为空并重复后面操作

//层序遍历
public void levelOrderTraversal(TreeNode root) {
    Queue<TreeNode> queue = new LinkedList<>();
    if (root == null) {
        return;
    }
    queue.offer(root);
    while (!queue.isEmpty()) {
        TreeNode node = queue.poll();
        System.out.println(node.val);
        if (node.left != null) {
            queue.offer(node.left);
        }
        if (node.right != null) {
            queue.offer(node.right);
        }
    }
}

三、树的性能分析
树是一种分层存储数据的数据结构，它有不同类型的树的结构。对于平衡的二叉搜索树，插入、删除和查找节点等操作的时间复杂度平均为O(log n)，最坏情况下为O(n)。遍历树的操作需要访问每个节点，时间复杂度为O(n)。树的常用方法是三大遍历和层序遍历。

四、树的案例分析

对称二叉树
1. 题目链接：对称二叉树
2. 例子：root = [1,2,2,3,4,4,3]
3. 解题思路：这道题就是写一个深度遍历，首先我们需要清除什么条件就返回，当遇到叶子结点时，即一直遍历到最后都没有发生 false ，那么就返回 true ，当遇到一个结点有左节点但没有右节点就不对称，返回 false ，当遇到两个值不同，那么也不对称，返回 false 。
4. 相关题解：

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root == null) {
            return true;
        }
        return dfs(root.left, root.right);
    }
    public boolean dfs(TreeNode left, TreeNode right) {
        if (left == null && right == null) {
            return true;
        }
        if (left == null || right == null) {
            return false;
        }
        if (left.val != right.val) {
            return false;
        }
        return dfs(left.left, right.right) && dfs(left.right, right.left);
    }
}

二叉树的最小深度
1. 题目链接：二叉树的最小深度
2. 例子：root = [3,9,20,null,null,15,7]
3. 解题思路：最小深度是从根节点到最近叶子节点的最短路径上的节点数量，那么我们遍历树的时候，就有以下几种情况，一是左右都为空，即遇到叶子结点，返回 1 ；二是遇到左结点为空或者右结点为空，那么就返回另一个不为空的结点的最小深度；三是两个都不为空是，就要比较两个结点它们之间较小的深度。
4. 相关题解：

class Solution {
    public int minDepth(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int left = minDepth(root.left);
        int right = minDepth(root.right);
        //这里当左右子树都为空是，高度为 0 + 0 + 1 = 1
        //当有一个不为 0 ，那么就存在一个子树，那么当前的子树的 left 或 right 一个为 0 ，那么当前子树最小的高度就为 left/right + 1
        return root.left == null || root.right == null ? left + right + 1 : Math.min(left,right) + 1;

    }
}

五、树的解题方法归纳总结

详解二叉树：二叉树的遍历、构建、深度、平衡以及路径

堆

在学习堆之前，我们需要先了解一下堆是什么，在操作系统中，它是存储动态分配的内存区域，需要程序员手动操作和管理它，而在数据结构中，它也称为二叉堆，它基于树结构，因为我们在树的构建中，我们希望树也能够排序，而堆的一种常见应用是堆排序算法。

一、堆的基本概念

堆的定义：
1. 这里讨论的是数据结构的二叉堆，而非内存的堆
2. 堆必须为完全二叉树，且堆分为大根堆（每个父节点元素都得大于他的左右节点）和小根堆（每个父节点元素都得小于他的左右节点）。
3. 一个堆可以用一个一维数组来描述，若父节点下标为 i ，则他的左子节点下标为 2i + 1 ，右子节点下标为 2i + 2 。
堆的基本术语：
2.1 下滤：把元素往下调整，时间复杂度为 O(logn)
2.2 上滤：把元素往上调整，时间复杂度为 O(logn) ，把元素插入到堆当中，每添加一个元素，则将其与父节点进行比较，如果新添加节点小于等于父节点，则添加元素到该位置；否则，继续向上寻找父节点，直到找到某个位置，使得位于该位置的新元素的值小于等于对应父节点的元素的值，并且将原位置上的元素一一向后挪动，也就是上滤
2.3 建堆：
2.4 自顶向下建堆法：上滤；时间复杂度是 O(nlogn)
2.5 自下而上建堆法：下滤，分为一个一个子树各自调整再调整总的，时间复杂度是 O(n)
堆在 Java 中的定义
3.1 这里我们首先定义两个成员变量：
- 1.int[] 类型的 heapArray 来表示堆存储元素的空间
- 2.int 类型的 capacity 来表示堆的大小
- 3.int 类型的 size 来表示堆中元素的个数
3.2 再构造一个构造函数，需要传入参数想要构建的堆的大小
3.3 然后是一些相关的操作

public class MyHeap {
    private int[] heapArray;
    private int capacity;
    private int size;

    public MyHeap(int capacity) {
        this.capacity = capacity;
        heapArray = new int[capacity];
        size = 0;
    }

    //堆是否为空
    public boolean isEmpty() {
        
    }

    //堆是否已满
    public boolean isFull() {
        
    }

    //堆中插入元素
    public void put(int value) {
        
    }

    //堆中删除元素
    public int remove() {
        
    }

    //堆化
    private void heapify(int index) {
        
    }

    //计算父节点的索引
    private int parent(int index) {
        
    }

    //交换左右子节点
    private void swap(int i, int j) {
        
    }
}

二、堆的基本操作：

基础操作在 Java 中的实现：
1.1 判断堆是否为空
- 想要判断堆是否为空，只需要判断当前数组中元素的个数是否仍旧为 0 即可
  以下是判断堆是否为空的代码：

//堆是否为空
public boolean isEmpty() {
    return size == 0;
}

1.2 判断堆是否已满
- 想要判断堆是否已满，只需要判断当前数组中元素的个数是否等于给堆定义的大小即可
以下是判断堆是否已满的代码：

//堆是否已满
public boolean isFull() {
    return size == capacity;
}

1.3 计算父节点的索引
- 想要计算父节点的索引，我们得知堆实际上是完全二叉树，便可以按照定义来计算出它的父节点的索引

//计算父节点的索引
private int parent(int index) {
    return (index - 1) / 2;
}

1.4 交换左右子节点

//交换左右子节点
private void swap(int i, int j) {
    int temp = heapArray[i];
    heapArray[i] = heapArray[j];
    heapArray[j] = temp;
}

1.5 给堆插入元素
- 想要给堆插入元素，首先我们需要判断堆中是否已满，于是调用判断函数，若没有满，其实就是上滤的过程。首先定一个 index 可以得出当前数组已存元素的个数，然后将元素存入数组相应的位置。然后循环判断目前的 index 是否大于 0 并且目前加入的元素它本身值的大小是否大于它的父节点的值的大小，这时也需要调用父节点的 index 的函数，如果大于，那么就需要将它们两个元素的值交换，循环判断，最后 size++
以下是给堆插入元素的代码：

//堆中插入元素
public void put(int value) {
    if (isFull()) {
        System.out.println("堆已满，无可增加元素的空间");
        return;
    }
    int index = size;
    heapArray[index] = value;
    while (index > 0 && heapArray[index] > heapArray[parent(index)]) {
        swap(index, parent(index));
        index = parent(index);
    }
    size++;
}

1.6 堆化
- 其实这个堆化就是建造大顶堆的过程，我们需要先传入一个参数，然后计算出参数左右子节点的索引，然后我们在左右子节点中选出一个最大的并且大于我们目前索引所对应的值，如果存在这样一个值，那么就让那个节点值跟我们的原先值交换，再以那个节点值作为索引重新构建大顶堆。
以下是堆化的代码：

//堆化
private void heapify(int index) {
    int large = index;
    int leftChild = 2 * index + 1;
    int rightChild = 2 * index + 2;
    if (leftChild < currentSize && heapArray[leftChild] > heapArray[large]) {
        large = leftChild;
    }
    if (rightChild < currentSize && heapArray[rightChild] > heapArray[large]) {
        large = rightChild;
    }
    if (large != index) {
        swap(index, large);
        heapify(large);
    }
}

1.7 在堆中删除元素
- 在堆中删除元素，首先我们需要判断堆中是否为空，如果为空就返回 -1 ，其实删除元素的过程就是下滤的过程，我们需要将第一个节点先保存下来，然后把最后一个索引的值赋值给第一个节点，然后将统计元素个数的 size-- ，再重新以第一个节点的索引来重新构建二叉树，最后将之前保存的节点返回。
以下是在堆中删除元素的代码：

//堆中删除元素
public int remove() {
    if (isEmpty()) {
        System.out.println("堆为空,无可删除元素");
        return -1;
    }
    int root = heapArray[0];
    heapArray[0] = heapArray[size - 1];
    size--;
    heapify(0);
    return root;
}

三、堆的性能分析
堆是一种特殊的树结构，也被称为二叉堆，它分为小根堆和大根堆。对于二叉堆，插入和删除元素的时间复杂度为O(log n)，查找最值的时间复杂度为O(1)。堆常用于优先队列、排序算法等。
四、堆的案例分析
这里其实题目大多是优先队列，可以直接点击相关知识了解并做相应题目。

优先队列

定义：优先队列是一种特殊的队列数据结构，其中每个元素都关联有一个优先级。与普通的先进先出（FIFO）队列不同，优先队列根据元素的优先级来确定出队顺序，优先级高的元素会先被处理。在 Java 中，PriorityQueue 是一个基于堆（Heap）的无界优先队列，默认情况下是小顶堆，元素按自然顺序（或提供的比较器）排序。
基础操作：
2.1 插入元素：插入到堆的尾部，然后使用上滤，时间复杂度为O(logn)
2.2 弹出最小元素：（用小根堆），然后将最后一个元素放到根节点，进行下滤操作重新调整小根堆，时间复杂度为O(logn)
相关题目

前 K 个高频元素
相关题解

class Solution {
    //    - 前 K 个高频元素
    //    输入: nums = [1,1,1,2,2,3], k = 2
    //    输出: [1,2]
    public int[] topKFrequent(int[] nums, int k) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }

        //这里使用Comparator来排序！！！从小到大排序, 是按照value值来排序
        PriorityQueue<Integer> queue = new PriorityQueue<>(new Comparator<Integer>() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return map.get(o1) - map.get(o2);
            }
        });

        //遍历，每次迭代把最大的放进去！
        for (Integer key : map.keySet()) {
            if (queue.size() < k) {
                queue.add(key);
            } else if (map.get(key) > map.get(queue.peek())) {
                //每遇到比他大的，堆顶的元素弹出！！！！
                queue.poll();
                queue.add(key);
            }
        }
        
        int[] res = new int[k];
        int index = 0;
        while (!queue.isEmpty()) {
            res[index++] = queue.poll();
        }
        return res;
    }
}

图论

一、图的基本概念
在学习图之前，我们首先要了解图本身的意思。在汉字中，图是古代在生物毛皮或者绢帕上绘制的关于边境城市或者各种边界结构的资料，而在计算机中，当我们需要表示像社交网络一样的关系的时候，就需要用到图。它被广泛应用于网络路由、社交网络分析、图像处理等领域。
1.图的定义：

图是由节点或者顶点和边组成的一种数据结构，用于描述物体之间的关系
图分为有向图和无向图两种类型。

2.基础概念：

度：顶点的度 TD(v) ，分为入度 ID(v) 和出度 OD(v)，入度是其他顶点指向当前顶点，出度是当前顶点指向其他顶点
路径：对无向图来说，是顶点之间的边，有向图中的路径也是有向的，即有箭头指向。
子图：类似子集，就是一个图拆分出来的多个子图。
连通图：顶点与顶点之间存在路径，则表明顶点之间是连通的。无向图中，如果任意两个顶点都是连通的，就是连通图。有向图中，如果存在顶点 a 到顶点 b 和顶点 b 到顶点 a 的路径，则称两个顶点之间是连通的，若任意两点之间都是连通的，则说明该图是强连通。
生成树：对连通的图进行遍历，即走路径，过程中所经过的边和顶点的组合把它看成一棵树，就称为生成树

3.图在 Java 中的定义
3.1 这里我们首先定义两个成员变量：
1. int 类型的 v 来表示顶点
2. List<List> 类型的 adjList 来存储边的集合
3.2 再构造一个构造函数，需要传入参数顶点：
1. 目的是初始化邻接表，为每个顶点创建一个空的列表。
3.3 图的相关操作

import java.util.ArrayList;
import java.util.List;

public class MyGraph {

    private int v;
    private List<List<Integer>> adjList;

    public MyGraph(int v) {
        this.v = v;
        adjList = new ArrayList<>(v);
        for (int i = 0; i < v; i++) {
            adjList.add(new ArrayList<>());
        }
    }

    //增加边
    public void addEdge(int source, int destination) {
        ......
    }

    //打印图
    public void printGraph() {
        ......
    }

}

二、图的基本操作：

基础操作在 Java 中的实现：
1.1 给图增加边

想要增加边，我们就需要传入两个顶点参数，然后在集合中添加这条边，因为是无向图，所以要添加两次。
以下是在图中增加边的代码：

//增加边
public void addEdge(int v1, int v2) {
    adjList.get(v1).add(v2);
    adjList.get(v2).add(v1);
}

1.2 打印图

打印图我们只需要将集合遍历。
以下是打印图的代码：

//打印图
public void printGraph() {
    for (int i = 0; i < v ; i++) {
        System.out.print("Vertex " + i + ": ");
        for (int temp : adjList.get(i)) {
            System.out.print(temp + " ");
        }
        System.out.println();
    }
}

三、图的存储

无向图的邻接矩阵
图例：
特点：
1. 无向图的邻接矩阵是对称的，且主对角线元素全为 0 (因为自己到自己没有边，即没有自环)。
2. 顶点 i 的度 = 第 i 行 (列) 中 1 的个数。
有向图的邻接矩阵
图例：
特点：
1. 有向图的邻接矩阵可能不是对称的。
2. 顶点的出度 = 第 i 行元素之和；
3. 顶点的入度 = 第 i 列元素之和；
4. 顶点的度 = 第 i 行元素之和 + 第 i 列元素之和。
无向图的邻接表：
图例：
特点：
1. 顶点 i 的度 = 第 i 个链表中除了他本身的结点个数。
有向图的邻接表：
图例：
特点：
1. 顶点 i 的出度为第 i 个链表中除了他本身的结点个数。

四、图的遍历

图的遍历是指从图中的任一顶点出发，对图中的所有顶点只访问一次
DFS: 深度优先遍历：
深度优先搜索是从起始节点出发，沿着一条路尽可能深地访问未访问的节点，直到尽头，然后回溯到上一个节点，继续搜索下一条路径。
BFS: 广度优先遍历：
广度优先搜索是从起始节点出发，访问当前节点的邻接点，直到遍历完所有节点。

四、图的案例分析
其实图论的问题考的比较多的还是深搜和广搜
1.所有可能的路径

题目：所有可能的路径
例子：graph = [[1,2],[3],[3],[]]
解题思路：深度优先遍历就是先进入第一个顶点，cnt 此时要加上 0 这个点，因为题目要求是从 0 开始，我们得知 0 指向 1 和 2 ，首先，cnt 集合加上 1 ，然后我们搜 1 这个顶点，这个顶点指向 3 ，那么 cnt 集合再加上 3 ，那么第一条路径就出来了， 0 1 3，然后回溯，将 3 删去，这时 1 没有其他链接的边，那么再删去 1 ，回溯到 0 这个顶点，index ++ , 到 2 ，然后继续重复之前的步骤，搜 2 ，最后得到第二条路径 0 2 3。
Java中实现（代码）：

class Solution {
    List<List<Integer>> res;
    List<Integer> cnt;
    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        res = new ArrayList<>();
        cnt = new ArrayList<>();
        cnt.add(0);
        dfs(graph, 0);
        return res;
    }
    public void dfs(int[][] graph, int node) {
        if (node == graph.length - 1) {
            res.add(new ArrayList<>(cnt));
            return;
        }
        for (int index = 0;index < graph[node].length;index++) {
            int newNode = graph[node][index];
            cnt.add(newNode);
            dfs(graph, newNode);
            cnt.remove(cnt.size()-1);
        }
    }
}

2.岛屿数量

题目：岛屿数量
例子：
grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
解题思路：看到岛屿问题，首先我们先定义方向数组，向上下左右走的数组，然后进入给我们的图，当遇到没访问的并且数值为 1 时，证明是陆地，那么我们就给他广度遍历。在广度遍历中，我们需要用到队列来辅助我们。首先将 1 的下标放入队列，然后把其标记为已访问，把队列的元素弹出，让这个下标去上下左右走，再标记。
Java中实现（代码）：

class Solution {
    int[][] des = { {0, 1}, {0, -1}, {1, 0}, {-1, 0} };
    boolean[][] visit;
    public int numIslands(char[][] grid) {
        int res = 0;
        visit = new boolean[grid.length][grid[0].length];
        for (int i = 0 ; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if (!visit[i][j] && grid[i][j] == '1') {
                    bfs(grid, i, j);
                    res++;
                }
            }
        }
        return res;
    }
    public void bfs(char[][] grid, int i, int j) {
        Queue<int[]> queue = new LinkedList<>();
        queue.add(new int[]{i, j});
        visit[i][j] = true;
        while (!queue.isEmpty()) {
            int[] temp = queue.poll();
            int x = temp[0];
            int y = temp[1];
            for (int a = 0 ; a < 4; a++) {
                int newX = x + des[a][0];
                int newY = y + des[a][1];
                if (newX < 0 || newY < 0 || newX == grid.length || newY == grid[0].length) {
                    continue;
                }
                if (!visit[newX][newY] && grid[newX][newY] == '1') {
                    queue.add(new int[]{newX, newY});
                    visit[newX][newY] = true;
                }
            }
        }
    }
}

深搜：深度优先搜索知识点题库 - 力扣（LeetCode）
广搜：广度优先搜索知识点题库 - 力扣（LeetCode）
leetcode题单：图知识点题库 - 力扣（LeetCode）