今天周赛 T4 的组合数卡了一个小时，于是参考网上的文章总结了各类情形的计算方法，分享在这里供大家讨论，如有问题也欢迎大家不吝赐教。也希望大家能贡献一些相关的题目验证以下各个方法。

---

参考文章：https://blog.csdn.net/qwb492859377/article/details/50654627

三个属性

一般的排列组合场景都可以抽象为「把球放入盒子」的问题。根据场景不同，球或盒子有以下性质：

• 球和球之间是否相同。
• 盒与盒之间是否相同。
• 放完之后，是否允许有空盒子。

组合以上性质，共有八种场景。

是否相同可以理解为是否考虑排列。比如，把六个球放入两个盒子里面，每个盒子各三个。

当球相同，盒相同时，显然只有一种方法(限制了每个盒子放三个)。

当球不同，盒相同时，显然有多种方法，比如：

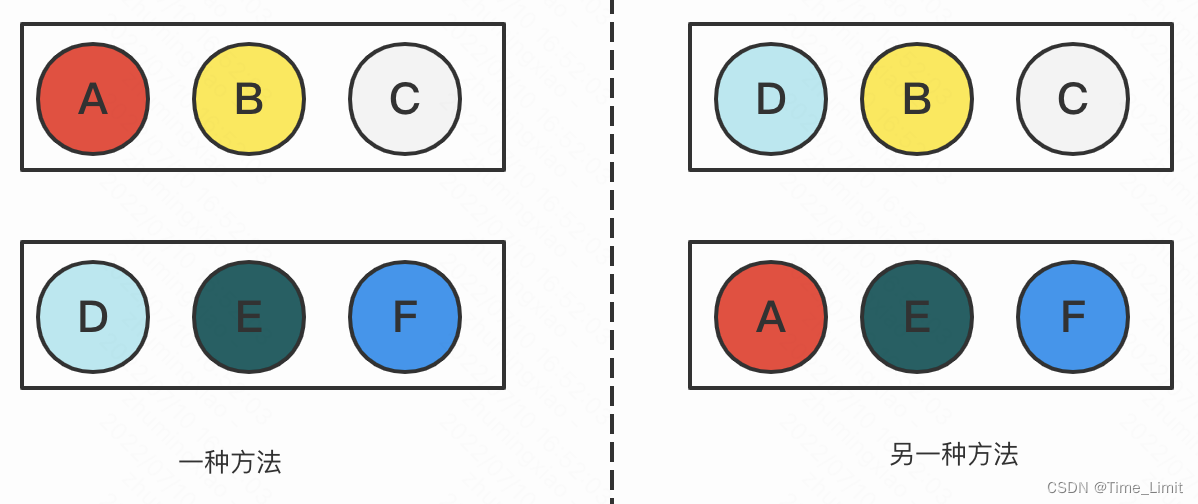
当球不同，盒不同时，显然也有多种方法，比如：

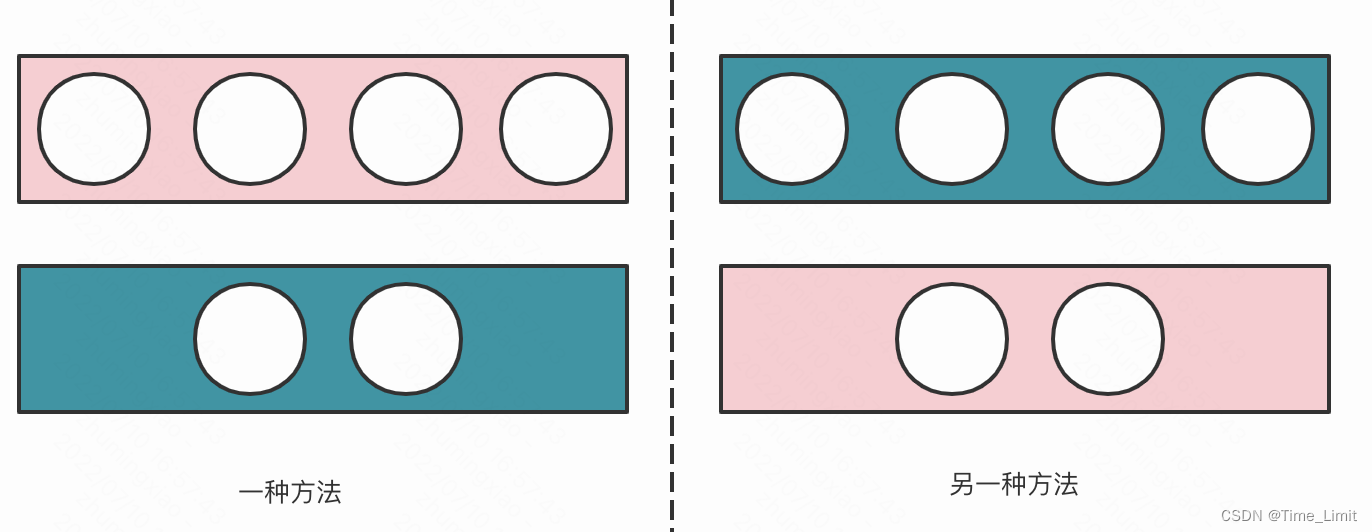
当球相同，盒不同时，显然也只有一种方法(限制了每个盒子放三个)：

但是当一个盒子放四个，另一个盒子放两个时，有两种方案：

一个约定：为了描述方便，我们设球的数量为 n ($n\ge 1$)，盒子的数量为 m ($m\ge 1$)。

情形一：球相同，盒相同，允许有空盒。

当 $n\le 1orm=1$ 时，这是递归的边界：「仅有一个球或没有球」或者「仅有一个盒子」，显然只有一种方法。

当 $n<m$ 时，至少有 $m-n$ 个盒子是空的，那就先把这些盒子丢弃吧。

当 $n\ge m$ 时，有两种策略：

• 丢掉一个盒子(注意，这个盒子可能在之前的步骤放过球了)。
• 每个盒子放一个球。

情形二：球相同，盒相同，无空盒。

可以基于「情形一」推演出来。先向每个盒子放一个球，保证无空盒，然后就变成了情形一。因此有：

情形三：球相同，盒不同，无空盒。

插板法：$n$ 个球依次排成一行，有 $n-1$ 个缝隙。有 $m-1$ 个隔板，将球分成 $m$ 份。相当于从 $n-1$ 个缝隙中挑选出 $m-1$ 个放置隔板。因此：

情形四：球相同，盒不同，允许有空盒。

等价于 $n+m$ 个球放入 $m$ 个盒子，不允许空。可以理解为：预先向 $m$ 个盒子各放入了一个球。因此有：

情形五：球不同，盒相同，无空盒。

解释一下：

• 当 $n<m$ 时，必然会有空盒子，因此为 $0$。
• 当 $n=m$ 时，每个盒子只能放一个，且盒子相同，所以只有 $1$ 中。
• 当 $n>m$ 时：
  • 如果前 $n-1$ 个球放入了 $m$ 个盒子，则第 $n$ 个球，有 $m$ 种放法；
  • 如果前 $n-1$ 个球放入了 $m-1$ 个盒子，则第 $n$ 个球只能放入剩余的空盒，因此只有 $1$ 种。
  • 如果前 $n-1$ 个球放入了 $m-2$ 或更少的盒子，则第 $n$ 个球无论咋放都会有空盒，因此为 $0$ 种。

情形六：球不同，盒相同，允许有空盒。

将该问题拆分为 $m$ 个子问题，每个子问题都变为了情形五。

情形七：球不同，盒不同，允许有空盒。

一共 $n$ 个球，每个球都有 $m$ 种放法，总共有 $n^m$。

情形八：球不同，盒不同，无空盒。

基于情形五计算。情形五中盒子是相同的，因此只需再乘上盒子的排列即可。答案为：