排序算法总结(C++) - 讨论 - 力扣（LeetCode）

排序算法总结(C++)

写代码的火车

1483

2022.06.15

发布于未知归属地

排序 C++学习分享

自己备忘用, 有错误请大佬指出

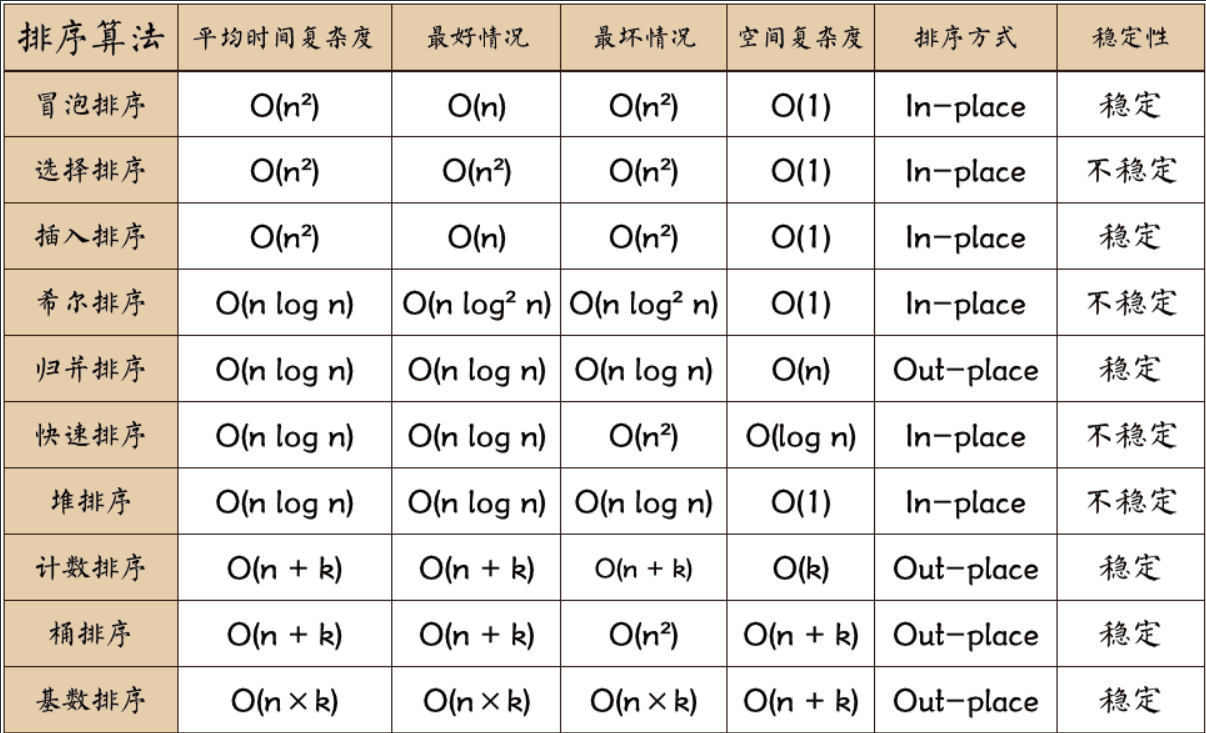
各排序复杂度表

冒泡排序

constexpr int N = 1e+5 + 10; 
int arr[N]; 

// n待排列数组的元素个数  
void bubbleSort(int n)
{
    for(int i = 0; i < n; ++i)
        for(int j = 0; j < n - 1 - i; ++j) 
            if(arr[j] > arr[j + 1]) swap(arr[j], arr[j + 1]); 
}

$空间复杂度 : O (1)$

$时间复杂度 : O (n^{2})$

$稳定排序算法$

可以改进, 但改进后, 最好情况是 $O (n)$ , 最坏还是 $O (n^{2})$

选择排序

constexpr int N = 1e+5 + 10; 
int arr[N]; 

// n待排列数组的元素个数  
void selectSort(int n)
{
    for(int i = 0; i < n; ++i) 
    {
        int t = i; 
        for(int j = i + 1; j < n; ++j) 
            if(arr[t] > arr[j]) t = j; 
        swap(arr[t], arr[i]); 
    }
}

$空间复杂度 : O (1)$

$时间复杂度 : O (n^{2})$

$非稳定排序算法$

插入排序

constexpr int N = 1e+5 + 10; 
int arr[N]; 

// n待排列数组的元素个数  
void insertSort(int n)
{
    for(int i = 1; i < n; ++i) 
    {
        int j = i, x = arr[i]; 
        while(j && arr[j - 1] > x) arr[j] = arr[j - 1], --j; 
        arr[j] = x; 
    }
    return; 
}

$空间复杂度 : O (1)$

$时间复杂度 : 最坏 O (n^{2}), 最好 O (n)$

$稳定排序算法$

希尔排序

constexpr int N = 1e+5 + 10; 
int arr[N]; 

// n待排列数组的元素个数  
void shellSort(int n)
{
    int gap = n / 2; 
    while(gap)
    {
        for(int i = gap; i < n; ++i) 
        {
            int j = i, x = arr[i]; 
            while(j >= gap && arr[j - gap] > x) arr[j] = arr[j - gap], j -= gap; 
            arr[j] = x; 
        }
        gap /= 2; 
    }
}

$空间复杂度 : O (1)$

$时间复杂度 :$

一般书上都说希尔排序的时间复杂度是 $O (n^{1.5})$ ，但是学过算法的都知道有最坏时间复杂度的，希尔排序的时间复杂度其实是和增列序列有关系的，即我们程序实现的步长，{1,2,4,8,...}这种序列就是我们程序中实现的这种，并不是很好的增量序列，使用这个增量序列的时间复杂度(最坏情形)是 $O (n^{2})$ ，Hibbard提出了另一个增量序列{1,3,7，..., $2^{k - 1}$ }(质数增量)，这种序列的时间复杂度(最坏情形)为 $O (n^{1.5})$ ，这个提高就很厉害了，只是修改一个算法的一个参数；Sedgewick提出了几种增量序列，其最坏情形运行时间为 $O (n^{1.3})$ ,其中最好的一个序列是{1,5,19,41,109,..}

$不稳定排序算法$

快速排序

constexpr int N = 1e+5 + 10; 
int arr[N]; 

// l为待排列数组的左端点, r为待排列数组的右端点  
void quickSort(int l, int r)
{
    if(l >= r) return; 
    int i = l - 1, j = r + 1, x = arr[l + r >> 1]; 
    while(i < j)
    {
        while(arr[++i] < x); 
        while(arr[--j] > x); 
        if(i < j) swap(arr[i], arr[j]); 
    }
    quick_sort(l, j); 
    quick_sort(j + 1, r); 
}

$空间复杂度 : O (1)$

$时间复杂度 : 最坏 O (n^{2}), 最好 O (n l o g_{2} n)$

$非稳定排序算法$

归并排序

constexpr int N = 1e+5 + 10; 
int arr[N], t[N];

// l为待排列数组的左端点, r为待排列数组的右端点  
void mergeSort(int l, int r)
{
    if(l >= r) return; 
    int mid = l + r >> 1; 
    merge_sort(l, mid);
    merge_sort(mid + 1, r); 
    int i = l, j = mid + 1, k = 0; 
    while(i <= mid && j <= r) 
        if(arr[i] <= arr[j]) t[k++] = arr[i++]; 
        else t[k++] = arr[j++];  
    while(i <= mid) t[k++] = arr[i++]; 
    while(j <= r) t[k++] = arr[j++]; 
    for(int i = l, j = 0; i <= r;  ++i, ++j) arr[i] = t[j]; 
}

$空间复杂度 : 最坏 O (n), 最好 O (l o g_{2} n)$

$时间复杂度 : 最坏 O (n^{2}), 最好 O (n l o g_{2} n)$

$稳定排序算法$

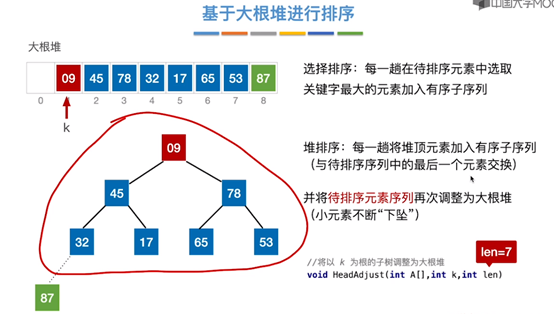
堆排序

constexpr int N = 1e+5 + 10; 
int h[N];

// 大顶堆下沉操作, x为进行下沉操作的位置下标, 该下标由 1 开始
void down(int x, int n)
{
    int t = x; 
    if(2 * x <= n && h[t] < h[2 * x]) t = 2 * x; 
    if(2 * x + 1 <= n && h[t] < h[2 * x + 1]) t = 2 * x + 1; 
    if(t != x) swap(h[x], h[t]), down(t, n);
}

// 将数组整理为大顶堆, n为元素个数 
void heapCreate(int n)
{
    // 从完全二叉树的第一个非叶子结点开始往前直到根结点, 依次进行下沉操作
    for(int i = n / 2; i; --i) down(i, n);    
}

// 堆排序, n为元素个数 
void heapSort(int n)
{
    while(n - 1)
    {
        swap(h[1], h[n]); 
        down(1, --n); 
    }
}

大顶堆 --> 升序
小顶堆 --> 降序

$空间复杂度 : O (1)$

$时间复杂度 : O (n) + O (n l o g_{2} n) = O (n l o g_{2} n), 其中 O (n) 为建堆时间, O (n l o g_{2} n) 为排序时间$

$非稳定排序算法$

计数排序

计数排序01

计数排序02

计数排序03

计数排序04

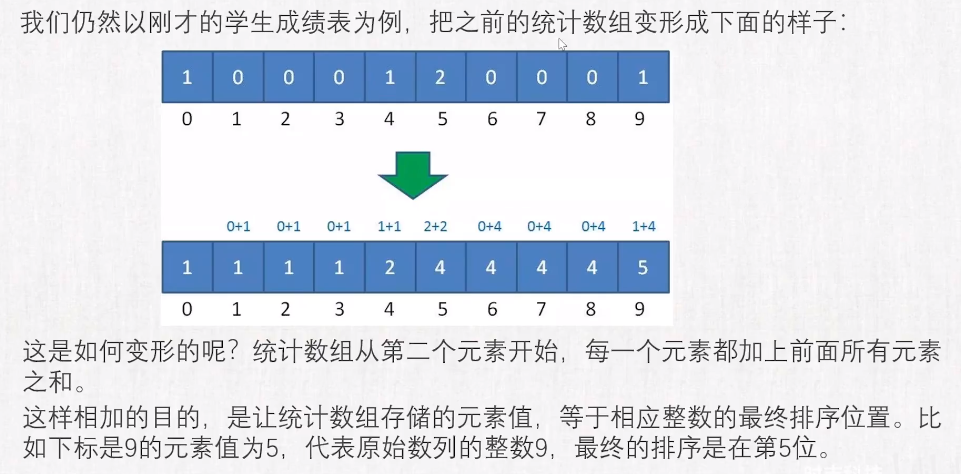
计数排序05

计数排序06

// 元素个数 100000, 元素的取值范围为 1 	~ 100000 
constexpr int N = 1e+5 + 10; 
int arr[N], cnts[N], res[N]; 


void countSort(int n)
{
    for(int i = 1; i <= n; ++i) cnts[arr[i]]++; 
    
    for(int i = 1; i < N ; ++i) cnts[i] += cnts[i - 1]; 
    for(int i = n; i; --i) res[cnts[arr[i]]--] = arr[i];  
}

// 元素个数 100000, 元素取值范围 1 ~ 10^9, 此时无法开辟这么大的静态数组 
// 这里可以用 C++ 的 map 容器, 来存储并求前缀和  
void countSort(int n)
{
    map<int, int> cnts;    
    for(int i = 1; i <= n; ++i) cnts[arr[i]]++; 
    int t = 0; 
    for(auto [k, v] : cnts) 
    {
        cnts[k] += t; 
        t += v; 
    }
    for(int i = n; i; --i) res[cnts[arr[i]]--] = arr[i];  
}

针对数据在一定范围内的情况, 且元素个数n较大的情况

$空间复杂度 : O (k), k 为元素的取值范围$

$时间复杂度 : O (n + k)$

$稳定排序算法$

基数排序

基数排序01

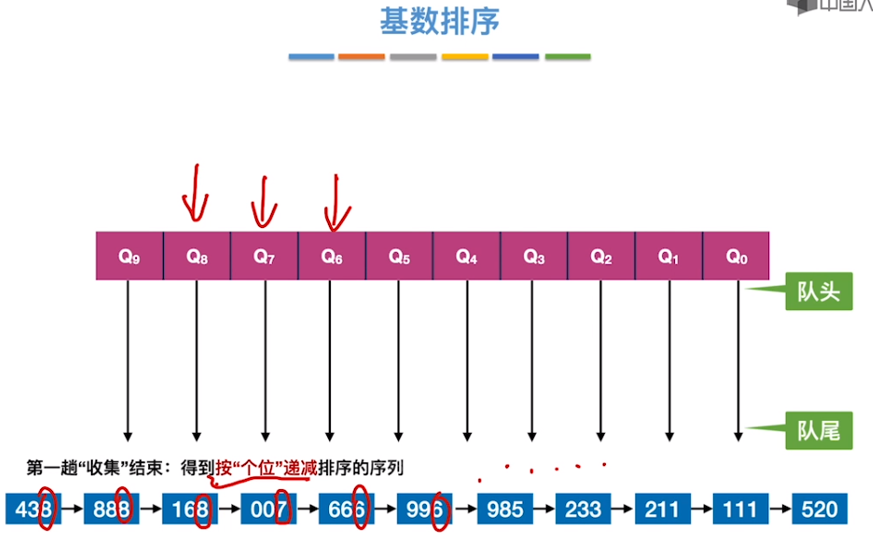
基数排序03

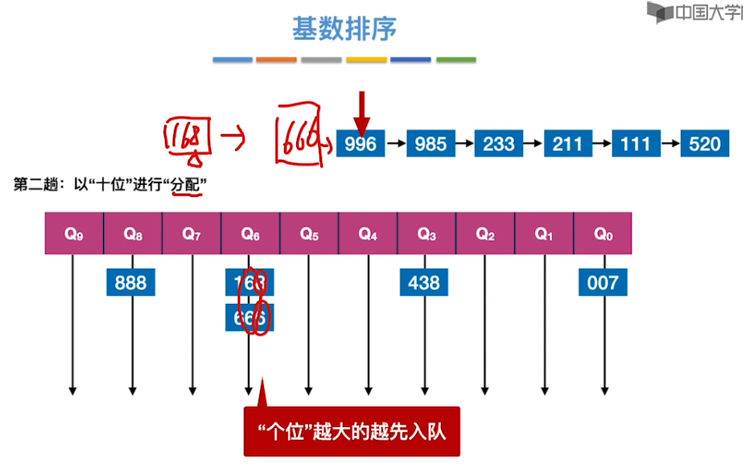
基数排序04

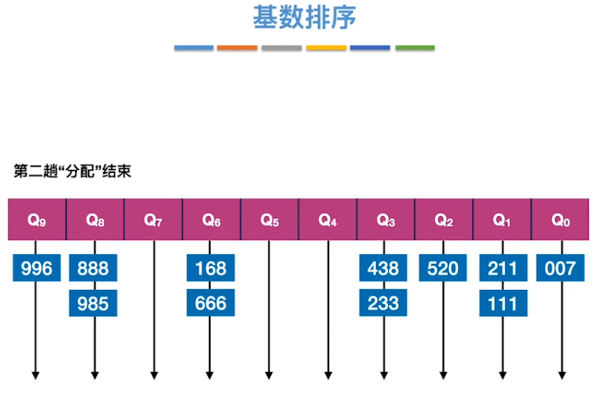
基数排序05

基数排序06

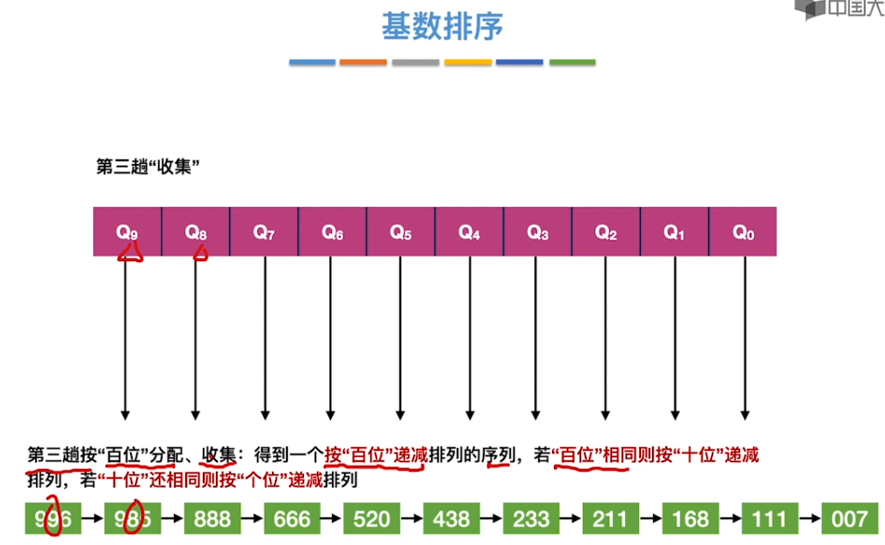
基数排序08

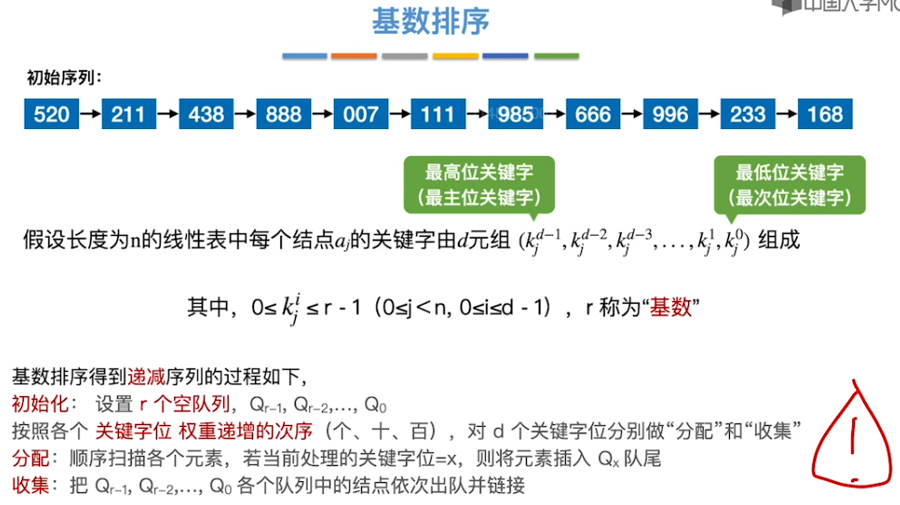
基数排序09

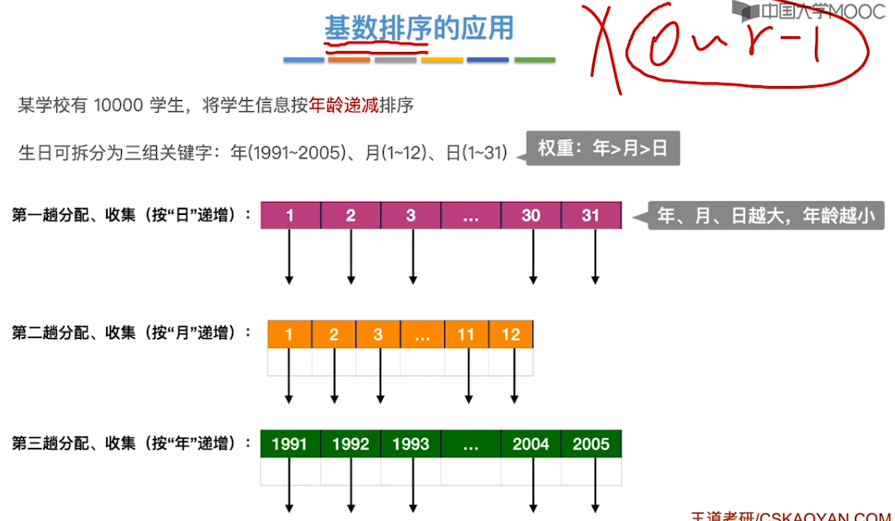
基数排序10

constexpr int N = 1e+5 + 10; 
int arr[N], b[10][N];         // b二维数组为收集队列, 第二维度的第一个元素存储元素个数 

void radixSort(int n)
{
    int base = 1; 
    for(int i = 0; i < 10; ++i) 
    {
        for(int j = 0; j < n; ++j) 
        {
            int t = arr[j] / base % 10; 
            b[t][++b[t][0]] = arr[j]; 
        }
        
        for(int j = 0, k = 0; j < 10; ++j) 
        {
            for(int x = 1; x <= b[j][0]; ++x) arr[k++] = b[j][x];  
            b[j][0] = 0; 
        }
        base *= 10; 
    }
}

$空间复杂度 : O(k), k为辅助队列

$时间复杂度 : O (d * (n + r)), 其中 d 为把关键字拆分为 d 个部分, r 表示每个部分有 r 个取值$

$稳定排序算法$

桶排序

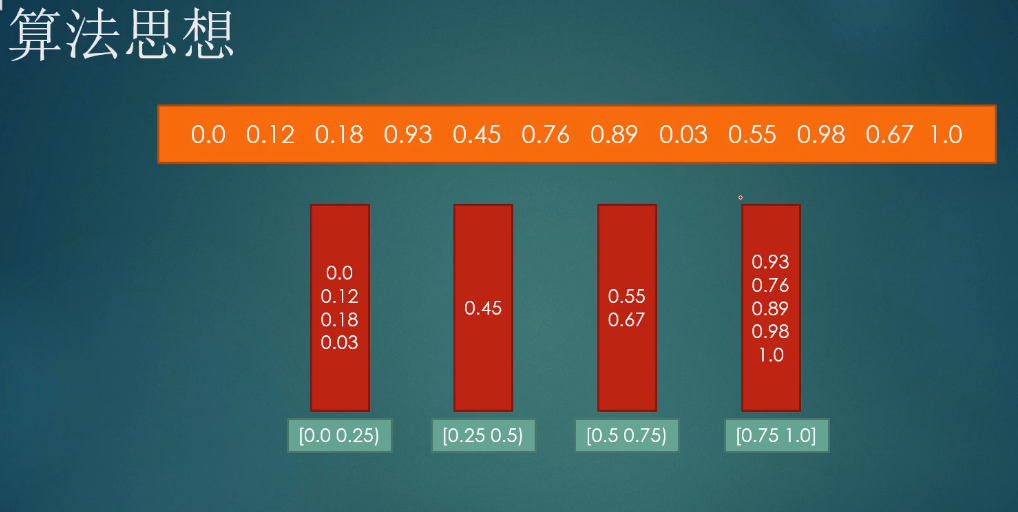
桶排序思想

计数排序和基数排序都是桶排序的特殊情况, 单独的桶排序用得不多, 桶排序可以解决计数和基数解决不了的小数或者负数之类的问题. 基于桶排序的算法, 需要特别注意常数项, 其常数项往往很大, 所以一般只适于一些特殊的场合