本次周赛还是具备一定的挑战性的,从后面两题来看,侧重点应该在于动态规划。前两题考察的还是基础的编程能力,这些只需要我们多编程实践,仔细阅读题意即可。
大概 30 分钟做完前三题,然后经过一个小时的努力,还是无法攻克第四题。但相信只要不断的思考总结,还是有可能打破"日常三题"的局面,毕竟也只有少数人能够第一次靠自己写出算法,更多的还是积累经验吧。
下文将会根据我的比赛思路以及大佬的帮助,对周赛题目进行分析。如果想更进一步提升自己,推荐查看相关题目的题解以及评论区,了解更多的解题技巧。
概要
- 第一题:模拟
- 第二题:模拟
- 第三题:dp
- 第四题:dp
5181. 公交站间的距离
在这个环形公交路线上,我们需要找到出发点 start 到目的地 destination 之间的最短距离。而路线只有两种情况,要么顺时针行驶,要么逆时针行驶。
因此,直接模拟这两种情况,顺时针加上当前下标的距离值,逆时针加上前一个下标的距离值,同时注意模拟过程中边界的处理。
代码如下:
public int distanceBetweenBusStops(int[] distance, int start, int destination) {
// ans 为顺时针结果,an2 为逆时针结果
int ans = 0, ans2 = 0;
// 顺时针模拟
int idx = start;
while (idx != destination) {
ans += distance[idx];
idx++;
// 循环模拟,下标等于数组长度时,重新指向第一个元素
if (idx == distance.length) {
idx = 0;
}
}
// 逆时针模拟
idx = start;
while (idx != destination) {
// 边界处理,下标等于 0 时,加上末尾的 distance
ans2 += idx == 0 ? distance[idx - 1] : distance[distance.length - 1];
idx--;
// 循环模拟,下标等于 -1 时,重新指向最后一个元素
if (idx == -1) {
idx = distance.length - 1;
}
}
// 最短距离
return Math.min(ans, ans2);
}5183. 一周中的第几天
嘿嘿,这道题目为了追求快,我偷偷调用了 API。
调用 API 的代码如下:
public String dayOfTheWeek(int day, int month, int year) {
String[] map = new String[]{"Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday"};
Calendar cal = Calendar.getInstance();
cal.set(year, month - 1, day);
return map[cal.get(Calendar.DAY_OF_WEEK) - 1];
}需要开头导包 import java.util.Calendar;
但在平时的做题中这种方案是不可取的,不推荐使用(比赛偷偷用就行)。
正确的解题思路是:从一个起点日期开始,计算起点到题目要求日期所经过的天数,最后加上起点所代表的星期下标,并对 7 进行取模,即不断循环天数,并映射到一周中的 7 天内。
代码如下:
// 月份与天数的映射,例如 1 月有 31 天
int a[]= new int[]{0,31,28,31,30,31,30,31,31,30,31,30,31};
// 判断闰年
public boolean run(int y) {
return (y % 4 == 0 && y % 100 != 0) || y % 400 == 0;
}
public String dayOfTheWeek(int day, int month, int year) {
String[] sa = new String[]{"Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday"};
// 起点是 1971/1/1 的前一天,星期四,即下标为 4
int sum = 4;
// 计算起点到题目给定日期经过的天数
// 遍历年份
for (int i = 1971; i < year; i++) {
sum += run(i) ? 366 : 365;
}
// 遍历月份
for (int i = 1; i < month; i++) {
if (i == 2) {
sum += run(year) ? 29 : 28;
} else {
sum += a[i];
}
}
// 遍历天数
sum += day;
// 映射到一周的 7 天
return sa[sum % 7];
}5182. 删除一次得到子数组最大和
这道题目还是有章可循的,事实上题库中也有相关的题目。当我第一眼看到这道题目的时候,差点被 删除 两个字劝退了,因为字符串的修改涉及的情况较多,一般比较难处理。
首先可以观察题目给定的数据规模:1 <= arr.length <= 10^5,一般来说是需要 或者 的解法,大部分情况下应该是 。而对于 的算法,有可能是动态规划或者贪心。
往着 的动态规划算法出发,由题目需要求子数组和来看,我们应该设计一个 dp[i],代表以 i 结尾的子数组。
并且,题目中规定每个子数组可以进行一次删除操作。那么,对于一个以 i 结尾的子数组,如果进行一次删除操作,删除的元素要么是 i 本身,要么是以 i - 1 结尾的字数组中的一个元素。
通过上述的分析,可以知道每个子数组应该具备两种状态,第一种状态为已经删除过一个元素,第二种状态为尚未删除过一个元素。
尚未删除过一个元素的状态可以通过以往求最大子数组和进行类似的求解,而已经删除过一个元素的状态由前一个子数组的两种状态决定。
状态转移方程如下:
// 0 代表 "尚未删除过一个元素" 状态
// 1 代表 "已经删除过一个元素" 状态
dp[i][0] = Math.max(arr[i], arr[i] + dp[i - 1][0]);
dp[i][1] = Math.max(dp[i - 1][1] + arr[i], dp[i - 1][0]);删除元素图示:

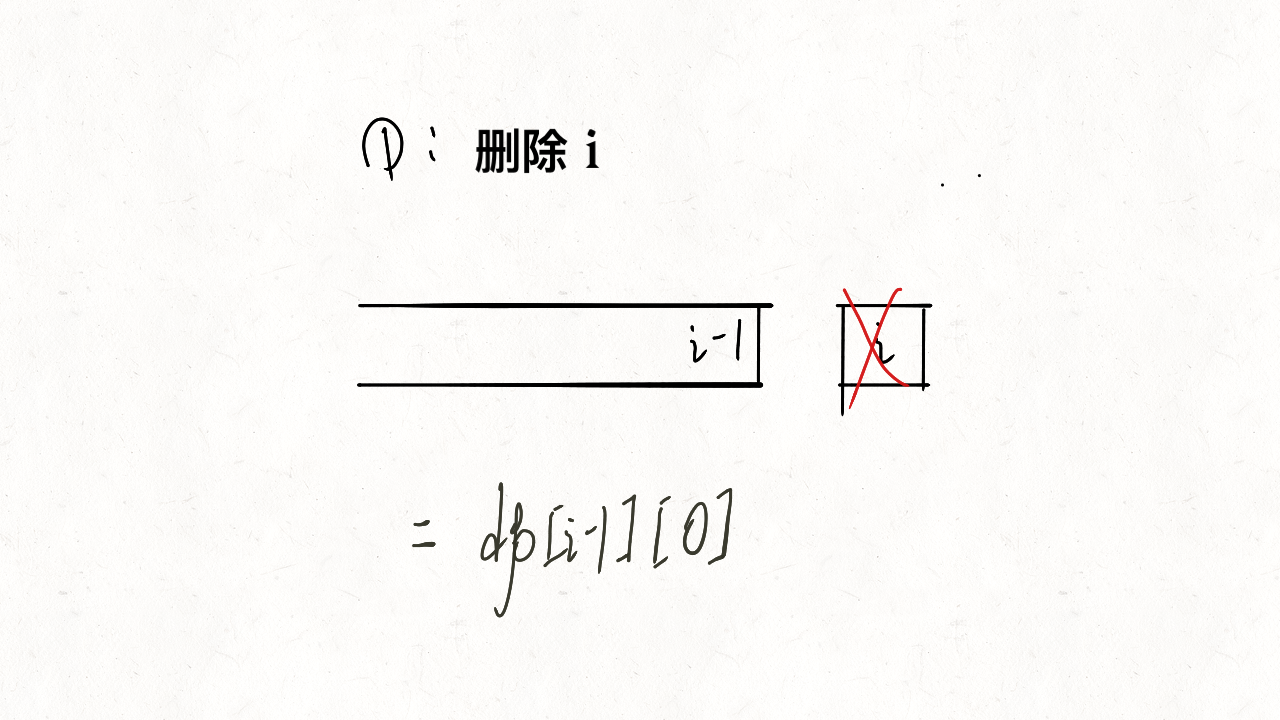

- 画的略丑,水平还不高,哈哈
- 注意:dp[i] 并不代表 i 元素一定存在
代码如下:
public int maximumSum(int[] arr) {
int ans = arr[0];
int len = arr.length;
int[][] dp = new int[len][2];
// 初始化状态
// "尚未删除",最大子数组和为本身
dp[0][0] = arr[0];
// "已经删除",只能删除自身,最大子数组和为 0
dp[0][1] = 0;
for (int i = 1; i < len; i++) {
// 如果前一个子数组和大于 0,则加上
dp[i][0] = Math.max(arr[i], arr[i] + dp[i - 1][0]);
// 删除的字符的两种情况:
// 1. 当前数字被删除,为了满足至少一个元素,必须加上前面一个子数组 "尚未删除" 的最大值
// 2. 当前数字不被删除,则由前面子数组删除,前面子数组 "已经删除" 的最大值加上当前数字
dp[i][1] = Math.max(dp[i - 1][1] + arr[i], dp[i - 1][0]);
// 两种状态都可能产生最大值
ans = Math.max(ans, dp[i][0]);
ans = Math.max(ans, dp[i][1]);
}
return ans;
}算法复杂度:,其中 N 是数组长度。
相关题目推荐:
在相关题目中,每一天都具备持有股票和未持有股票两种状态,而每一天都与前一天具备一定的关系。与本次的周赛题目思想基本一致,我也是通过这道题目所得到的启发。
5184. 使数组严格递增
思路来自拿过两块金的小白二号,相较常规的解法,比较难想到,但他本人基本上是秒杀的,或许这就是大佬吧。
定义一个 dp[i],代表 [0 ~ i] 保持 i 元素存在的最小「操作」数。
dp[i] = min{dp[j] + (i - j - 1)},其中 j < i, arr[j] < arr[i],(i - j - 1) 为替换的元素个数。被替换元素的下标从 j + 1 到 i - 1,所需要的替换元素 arr[k] 满足 arr[j] < arr[k] < arr[i]。
对题目中的替换数组 arr2 预处理,过滤重复元素,并进行排序。则可以在 通过二分查找判断是否可以进行替换。
但算出所有的 dp[i],我们会发现好像哪里有点问题。
第一个问题,最后一个元素不一定要保持,它可能也被替换,因此直接返回最后一个 dp[i] 可能会出现 BUG。只需要在 arr1 最后加上一个特别大的数字,然后考虑这个数字不被替换,则可以间接考虑原数组最后一个元素是否替换的两种情况。
第二个问题,对于上述提到的 dp[i] = min{dp[j] + (i - j - 1)},并无法考虑第一个元素被替换的情况。因为我们最后 dp[j] 只遍历到 dp[0],而 dp[0] 代表第一个元素不被替换。和第一个问题解法差不多,在 arrr1 开头加上一个特别小的数字,则可以间接考虑到原数组第一个元素被替换的情况。
代码如下:
// a1 为新扩展的 arr1,即开头和结尾加上两个元素
// a2 为预处理后的 arr2
int[] a1, a2;
public int makeArrayIncreasing(int[] arr1, int[] arr2) {
int len = arr1.length;
int ans = Integer.MAX_VALUE;
int[] dp = new int[len + 2];
// 预处理 arr1 和 arr2,得到新的 a1 和 a2
a1 = new int[arr1.length + 2];
// 开头加上很小的数字
a1[0] = -1;
for (int i = 1; i <= len; i++) {
a1[i] = arr1[i - 1];
}
// 结尾加上很大的数字
a1[len + 1] = 2000000000;
// 去重和排序 arr2
a2 = solve(arr2);
//
for (int i = 1; i <= len + 1; i++) {
dp[i] = Integer.MAX_VALUE;
for (int j = 0; j < i; j++) {
// a[j] 必须满足 a[j] < a[i],并且 dp[j] 可解,即可以保持 j 元素存在并且数组递增
if (a1[i] <= a1[j] || dp[j] == Integer.MAX_VALUE) {
continue;
}
// 判断是否可以成功替换
if (find(j, i)) {
dp[i] = Math.min(dp[i], dp[j] + (i - j - 1));
}
}
}
return dp[len + 1] == Integer.MAX_VALUE ? -1 : dp[len + 1];
}
// 预处理,去重 + 排序
public int[] solve(int[] arr) {
Set<Integer> set = new HashSet<>();
for (int a : arr) {
set.add(a);
}
int[] ans = new int[set.size()];
int idx = 0;
for (Integer a : set) {
ans[idx++] = a;
}
Arrays.sort(ans);
return ans;
}
// 判断是否可以进行替换
public boolean find(int j, int i) {
// 如果 j 和 i 相邻,则之间不存在元素,不需要替换
if (j + 1 == i) {
return true;
}
// 找到大于 a1[j] 的元素的最小下标 minIdx
// 找到小于 a1[i] 的元素的最大下标 maxIdx
int minIdx = bs(a1[j], a2), maxIdx = bs2(a1[i], a2);
if (minIdx == a2.length || maxIdx == -1) {
return false;
}
// 判断替换数组中满足替换要求的元素数量 是否大于 所需要的被替换元素数量
return (i - j - 1) <= (maxIdx - minIdx + 1);
}
// 找到第一个大于 t 的元素的下标,没有则返回数组长度
public int bs(int t, int[] nums) {
int l = 0, h = nums.length - 1;
while (l <= h) {
int m = l + (h - l) / 2;
if (nums[m] > t) {
h = m - 1;
} else if (nums[m] <= t) {
l = m + 1;
}
}
return l;
}
// 找到最后一个小于 t 的元素的下标,没有则返回 -1
public int bs2(int t, int[] nums) {
int l = 0, h = nums.length - 1;
while (l <= h) {
int m = l + (h - l) / 2;
if (nums[m] >= t) {
h = m - 1;
} else if (nums[m] < t) {
l = m + 1;
}
}
return h;
}以上代码看起来较长,但实际上套用了两个二分的模板,有效编写的仅为 makeArrayIncreasing() 函数和 solve() 函数。后续我会整理一份关于二分的文章,并附上相关的模板。
算法复杂度:,其中 N 是 arr1 的长度,M 是 arr2 的长度。
结尾
欢迎大家一键三连,点赞,收藏,关注。只要有时间,每周都会献上一份题解,O(∩_∩)O。
