提示:报告只包含基本解题思路,如果需要样例代码,请访问参考代码
https://github.com/chlxydl/LeetCodeWeeklyContest
Easy 5189. “气球” 的最大数量
题目
给你一个字符串 text,你需要使用 text 中的字母来拼凑尽可能多的单词 "balloon"(气球)。
字符串 text 中的每个字母最多只能被使用一次。请你返回最多可以拼凑出多少个单词 "balloon"。
题目解析
显然,拼凑出 N 个 "balloon"需要的字母个数需要满足:cnt['b']>=N, cnt['a']>=N, cnt['l']>=2N, cnt['o']>=2N, cnt['n']>=N。
因此,我们遍历一遍字符串,得到数组中这5个字符出现的次数cnt['a'],cnt['b'],cnt['l'],cnt['o'],cnt['n'],则能拼凑出来的最多单词数N为min(cnt['a'],cnt['b'],cnt['l']//2,cnt['o']//2,cnt['n'])。
分析一下时间复杂度,由于只需要遍历一遍字符串,因此时间复杂度为O(N),这里的N为字符串的长度。
Medium 5190. 反转每对括号间的子串
题目
给出一个字符串 s(仅含有小写英文字母和括号)。
请你按照从括号内到外的顺序,逐层反转每对匹配括号中的字符串,并返回最终的结果。
注意,您的结果中不应包含任何括号。
题目解析
题目描述中说明需要逐层反转,对于给出的例子"(u(love)i)",我们首先找到最外层的一对括号,对里头的内容"u(love)i"进行反转得到"i(evol)u",接着我们再从上一步得到的字符串中找到最外层的一对括号,对里头的内容"evol"进行反转得到"love"。每次找到字符串中最外层的一对括号,对里头的内容进行反转的操作是通用的,这是一个典型的递归方法。
我们来思考如何进行递归,对于给定的字符串s:
- 找到第一个左括号
(,计数器cnt=1。 - 从左括号的位置向右遍历,碰到
(则cnt+=1,否则cnt-=1。 - 如果
cnt=0,则当前区间为一个合法的括号序列,记区间为[l,r] s[:l]是不用处理的,我们递归s[l+1:r-1]和s[r+1:]得到结果,然后将三段结果连接起来,注意反转结果字符串。
最后分析一下时间复杂度,极限情况下,如果括号是全部是嵌套的,那么中间的字符串可能会被翻转N次,所以总的时间复杂度是O(N^2)。
思考:如何用栈解决该问题?时间复杂度如何?欢迎私信分享。
Medium 5191. K 次串联后最大子数组之和
题目
给你一个整数数组 arr 和一个整数 k。
首先,我们要对该数组进行修改,即把原数组 arr 重复 k 次。
举个例子,如果 arr = [1, 2] 且 k = 3,那么修改后的数组就是 [1, 2, 1, 2, 1, 2]。举个例子,如果 arr = [1, 2] 且 k = 3,那么修改后的数组就是 [1, 2, 1, 2, 1, 2]。
然后,请你返回修改后的数组中的最大的子数组之和。
注意,子数组长度可以是0,在这种情况下它的总和也是0。
由于 结果可能会很大,所以需要 模(mod) 10^9 + 7 后再返回。
题目解析
暴力解法
最近的周赛好像特别中意最大子段和问题,我们上期周赛也有类似的题目,不了解最大子段和问题的同学可以先看看[[1]][最大子段和]。我们可以先考虑一下最简单的做法,既然是数组重复K次,我们可以直接将arr展开k次,暴力求最大子段和。
#最大子段和
ans = 0
cur_sum = 0
for i in range(k):#我们不需要真的暴力展开arr
for a in arr:
cur_sum += a
if cur_sum < 0:
cur_sum = 0
ans = max(ans,cur_sum)这样,时间复杂度为O(N*k),其中N为arr长度,根据题目给的数据范围,N*k≈10^9。一般的,如果时间复杂度算出来的最大值超过10^8,程序就有超时的风险了,所以该做法虽然正确,但是复杂度是偏高的。
O(N)解法
由于原始数组是由arr重复k次得到,我们先来思考k=1和2的情况。显然k<3的时候我们可以直接按照暴力解法得到结果。那么对于重复3次或3次以上的情形,我们的结果会如下图所示:
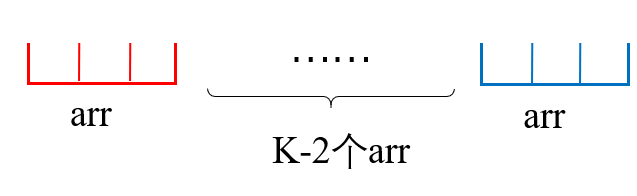
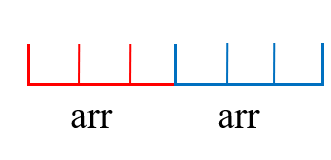
中间的arr会整体重复若干次,我们考虑sum(arr),如果sum(arr)<=0,由于中间的值都是负数,我们显然可以直接将其去掉而只保留首尾:
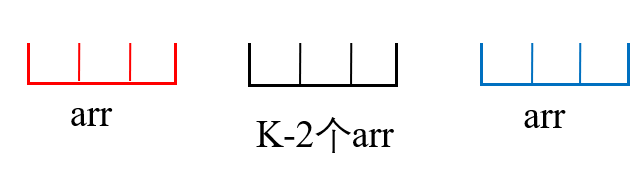
而如果sum(arr)> 0,中间的arr整体则需要尽量多的保留(k-2个),因为加上这些显然是可以继续增大我们的最大子段和的:
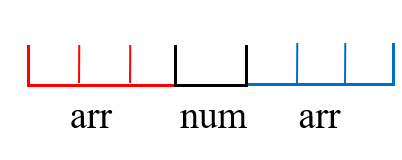
那么中间的重复部分做法就很明确了,我们根据他的和是否大于0来决定我们是需要保留0个还是保留k-2个,然后我们可以将中间的部分替换为一个数,也就是他的和:
最后,我们只需要在这个新的数组上求最大子段和就可以了。
来分析时间复杂度,由于我们真正计算最大子段和的数组长度最多为N*2+1,所以时间复杂度为O(N)。
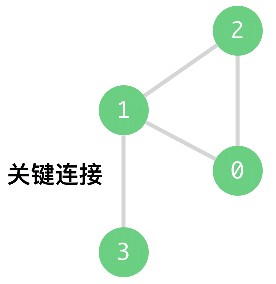
Hard 5192. 查找集群内的「关键连接」
提示:hard难度的题目在面试中比较少见,也相对复杂,如果准备时间不够可以跳过
题目
力扣数据中心有 n 台服务器,分别按从 0 到 n-1 的方式进行了编号。
它们之间以「服务器到服务器」点对点的形式相互连接组成了一个内部集群,其中连接 connections 是无向的。
从形式上讲,connections[i] = [a, b] 表示服务器 a 和 b之间形成连接。任何服务器都可以直接或者间接地通过网络到达任何其他服务器。
「关键连接」是在该集群中的重要连接,也就是说,假如我们将它移除,便会导致某些服务器无法访问其他服务器。
请你以任意顺序返回该集群内的所有 「关键连接」。
题目解析
对于在准备面试的同学来说,这道题相对来说考察的概率较小。他考察的知识点是如何在一个无向图中找“桥”,也就是割边。
首先简单介绍一下什么是割边,我们知道在一个连通图中,总会存在一些点和边,如果你删除了这个点或者边以后,原图就不连通了,那么这些点和边我们也分别叫做割点和割边。
这个问题也有很大的现实意义,比如说我们想评价一个网络是否健康,就可以用类似的做法查找里面是不是有一旦崩溃就会导致整个网络不连通的节点,如果有的话就考虑增加一些链接来提升鲁棒性。
暴力解法
对于这道题,有一个简单的思路是我们可以枚举每条边,然后删除这条边判断原图是否还连通,这样我们需要遍历删除的边O(M),然后遍历原图O(M),因此时间复杂度为O(M^2)。
O(M)解法
由于相关知识点就面试来说偏冷门,网上也已经有很多详细的讲解,这里不对知识点本身做详细说明。
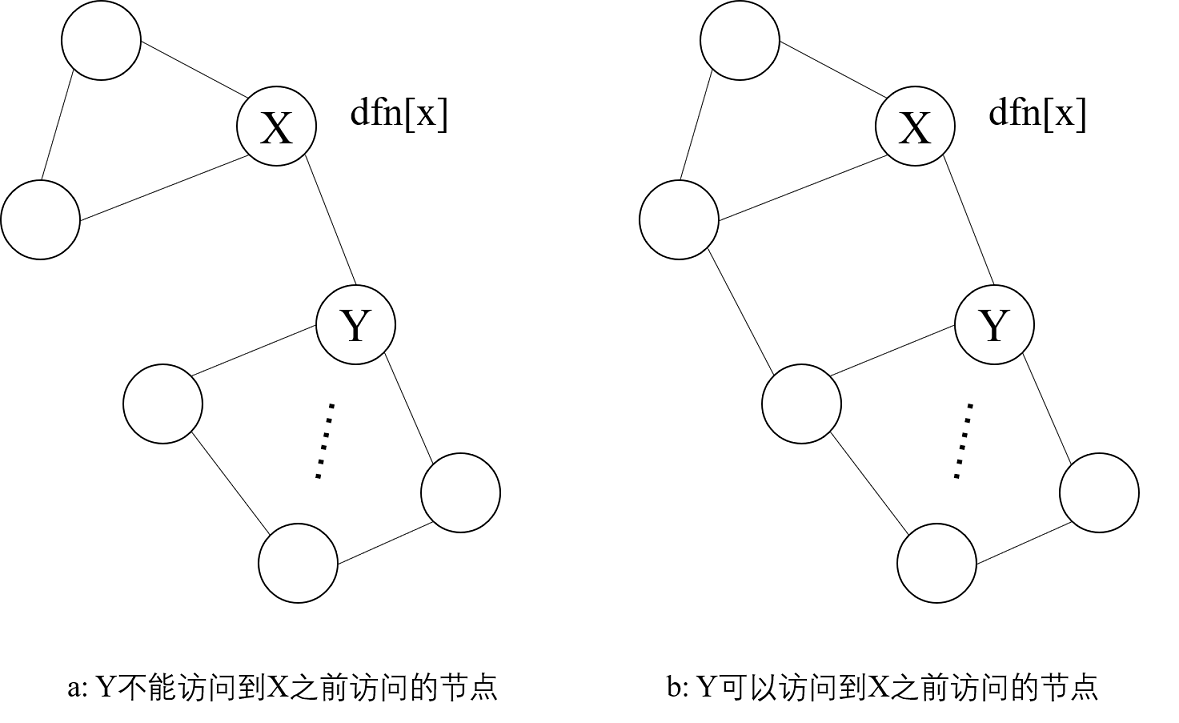
对于在图中找割边的问题,比较著名的算法就是Tarjan算法[[2]][Tarjan算法],tarjan为每个节点定义了dfn和low两个属性,其中dfn为dfs(深度优先搜索)时第一次访问的时间戳,low为从该节点出发,能访问到的最小的时间戳。
算法开始时,我们取任一个节点进行dfs,如果一个节点x是第一次访问到,那么其时间戳则为当前最大时间戳加一。接着我们遍历x能到达的点y,对y继续进行dfs。
我们考虑一下从y能到达的最小时间戳,如果y到达的最小时间戳大于x的时间戳,那么说明我们从y到达不了x之前访问的任何一个点,那么边x→y是桥。反之,则该边不是桥。详细过程请参考代码。
PS:这道题用python可能会超时,TLE的小伙伴们还是老老实实用C++吧~
[1]最大子段和
https://leetcode-cn.com/problems/maximum-subarray/
[2]Tarjan算法https://zh.wikipedia.org/wiki/Tarjan%E7%AE%97%E6%B3%95
https://leetcode-cn.com/problems/maximum-subarray/
