前言
一方面,受到 @观铃 🔔 的 启发 ,觉得这种形式的分享很有意义;
另一方面,模板库里的线段树感觉很多又很乱,缺少统一的标准(主要是以前缺乏对线段树本质的理解导致的)。按照 atcoder 模板库 的风格,使用 typescript 重构了一遍,并结合力扣的题目给出了使用案例,旨在提供一个可复用、高效率的线段树模板的设计参考,并理清线段树的学习路线和方向。
一些模板上的说明和例题,会慢慢补充上来

typescript 模板及使用案例
-
区间范围统一左闭右开,从 0 开始.
-
构造函数:
以区间修改区间查询的线段树为例.
构造函数说明
(
nOrLeaves: number | ArrayLike<E>,
operations: {
/**
* 线段树维护的值的幺元.
*/
e: () => E
/**
* 更新操作/懒标记的幺元.
*/
id: () => Id
/**
* 合并左右区间的值.
*/
op: (e1: E, e2: E) => E
/**
* 父结点的懒标记更新子结点的值.
*/
mapping: (lazy: Id, data: E) => E
/**
* 父结点的懒标记更新子结点的懒标记(合并).
*/
composition: (parentLazy: Id, childLazy: Id) => Id
}
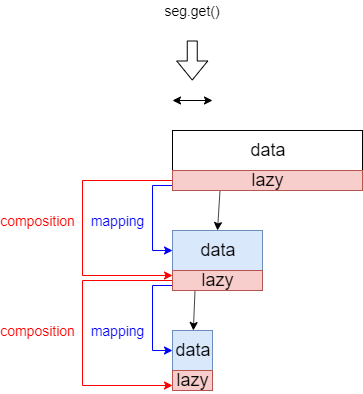
)线段树由以下七个部分唯一确定:
- E: 线段树维护的值(data)的类型.
- Id: 懒标记(lazy)的类型.
- e(): 线段树维护的值的幺元函数.
- id(): 懒标记的幺元函数.
- op(e1, e2): 合并左右区间的值的函数,结合律.
- mapping(lazy,data): 父结点的懒标记更新子结点的值的函数.
- composition(parentLazy,childLazy): 父结点的懒标记更新(结合)子结点的懒标记的函数.
可以参考下面两张图理解.

- 类方法命名:
- build(nums) : 从 nums 数组构造线段树.
- set(index,value) : 将 index 处的值更改为 value.
- get(index) : 获取 index 处的值.
- update(index,value)/updateRange(start,end,value) : 将范围内的值与 value 进行作用.
- query(start,end) : 查询范围内的聚合值.
- queryAll() : 查询整个线段树的聚合值.
- maxRight(start,predicate) :树上二分查询最大的
end使得[start,end)内的值满足predicate函数. - minLeft(end,predicate) :树上二分查询最小的
start使得[start,end)内的值满足predicate函数.
1.单点修改区间查询
SegmentTreePointUpdateRangeQuery
class SegmentTreePointUpdateRangeQuery<E = number> {
private readonly _n: number
private readonly _size: number
private readonly _data: E[]
private readonly _e: () => E
private readonly _op: (a: E, b: E) => E
/**
* 单点更新,区间查询的线段树.
* @param nOrLeaves 大小或叶子节点的值.
* @param e 幺元.
* @param op 结合律.
*/
constructor(nOrLeaves: number | ArrayLike<E>, e: () => E, op: (a: E, b: E) => E) {
const n = typeof nOrLeaves === 'number' ? nOrLeaves : nOrLeaves.length
let size = 1
while (size < n) size <<= 1
const data = Array(size << 1)
for (let i = 0; i < data.length; i++) data[i] = e()
this._n = n
this._size = size
this._data = data
this._e = e
this._op = op
if (typeof nOrLeaves !== 'number') this.build(nOrLeaves)
}
set(index: number, value: E): void {
if (index < 0 || index >= this._n) return
index += this._size
this._data[index] = value
while ((index >>= 1)) {
this._data[index] = this._op(this._data[index << 1], this._data[(index << 1) | 1])
}
}
get(index: number): E {
if (index < 0 || index >= this._n) return this._e()
return this._data[index + this._size]
}
/**
* 将`index`处的值与作用素`value`结合.
*/
update(index: number, value: E): void {
if (index < 0 || index >= this._n) return
index += this._size
this._data[index] = this._op(this._data[index], value)
while ((index >>= 1)) {
this._data[index] = this._op(this._data[index << 1], this._data[(index << 1) | 1])
}
}
/**
* 查询区间`[start,end)`的聚合值.
* 0 <= start <= end <= n.
*/
query(start: number, end: number): E {
if (start < 0) start = 0
if (end > this._n) end = this._n
if (start >= end) return this._e()
let leftRes = this._e()
let rightRes = this._e()
for (start += this._size, end += this._size; start < end; start >>= 1, end >>= 1) {
if (start & 1) leftRes = this._op(leftRes, this._data[start++])
if (end & 1) rightRes = this._op(this._data[--end], rightRes)
}
return this._op(leftRes, rightRes)
}
queryAll(): E {
return this._data[1]
}
/**
* 树上二分查询最大的`end`使得`[start,end)`内的值满足`predicate`.
* @alias findFirst
*/
maxRight(start: number, predicate: (value: E) => boolean): number {
if (start < 0) start = 0
if (start >= this._n) return this._n
start += this._size
let res = this._e()
while (true) {
while (!(start & 1)) start >>= 1
if (!predicate(this._op(res, this._data[start]))) {
while (start < this._size) {
start <<= 1
if (predicate(this._op(res, this._data[start]))) {
res = this._op(res, this._data[start])
start++
}
}
return start - this._size
}
res = this._op(res, this._data[start])
start++
if ((start & -start) === start) break
}
return this._n
}
/**
* 树上二分查询最小的`start`使得`[start,end)`内的值满足`predicate`
* @alias findLast
*/
minLeft(end: number, predicate: (value: E) => boolean): number {
if (end > this._n) end = this._n
if (end <= 0) return 0
end += this._size
let res = this._e()
while (true) {
end--
while (end > 1 && end & 1) end >>= 1
if (!predicate(this._op(this._data[end], res))) {
while (end < this._size) {
end = (end << 1) | 1
if (predicate(this._op(this._data[end], res))) {
res = this._op(this._data[end], res)
end--
}
}
return end + 1 - this._size
}
res = this._op(this._data[end], res)
if ((end & -end) === end) break
}
return 0
}
build(arr: ArrayLike<E>): void {
if (arr.length !== this._n) throw new RangeError(`length must be equal to ${this._n}`)
for (let i = 0; i < arr.length; i++) {
this._data[i + this._size] = arr[i] // 叶子结点
}
for (let i = this._size - 1; i > 0; i--) {
this._data[i] = this._op(this._data[i << 1], this._data[(i << 1) | 1])
}
}
toString(): string {
const sb: string[] = []
sb.push('SegmentTreePointUpdateRangeQuery(')
for (let i = 0; i < this._n; i++) {
if (i) sb.push(', ')
sb.push(String(this.get(i)))
}
sb.push(')')
return sb.join('')
}
}典型题目:
2213. 由单个字符重复的最长子字符串
2407. 最长递增子序列 II
2444. 统计定界子数组的数目
2736. 最大和查询
type E = {
size: number
preMax: number
sufMax: number
max: number
leftChar: string
rightChar: string
}
function longestRepeating(s: string, queryCharacters: string, queryIndices: number[]): number[] {
const n = s.length
const leaves: E[] = Array(n)
for (let i = 0; i < n; i++) {
leaves[i] = { size: 1, preMax: 1, sufMax: 1, max: 1, leftChar: s[i], rightChar: s[i] }
}
const seg = new SegmentTreePointUpdateRangeQuery<E>(
leaves,
() => ({
size: 0,
preMax: 0,
sufMax: 0,
max: 0,
leftChar: '',
rightChar: ''
}),
(a, b) => {
const res = {
size: a.size + b.size,
leftChar: a.leftChar,
rightChar: b.rightChar,
preMax: 0,
sufMax: 0,
max: 0
}
if (a.rightChar === b.leftChar) {
res.preMax = a.preMax
if (a.preMax === a.size) res.preMax += b.preMax
res.sufMax = b.sufMax
if (b.sufMax === b.size) res.sufMax += a.sufMax
res.max = Math.max(a.max, b.max, a.sufMax + b.preMax)
} else {
res.preMax = a.preMax
res.sufMax = b.sufMax
res.max = Math.max(a.max, b.max)
}
return res
}
)
const res: number[] = Array(queryIndices.length)
for (let i = 0; i < queryIndices.length; i++) {
const pos = queryIndices[i]
const char = queryCharacters[i]
seg.set(pos, { size: 1, preMax: 1, sufMax: 1, max: 1, leftChar: char, rightChar: char })
res[i] = seg.queryAll().max
}
return res
}2.区间修改单点查询
SegmentTreeRangeUpdatePointGet
class SegmentTreeRangeUpdatePointGet<Id = number> {
private readonly _n: number
private readonly _size: number
private readonly _height: number
private readonly _lazy: Id[]
private readonly _id: () => Id
private readonly _composition: (f: Id, g: Id) => Id
private readonly _equalsToId: (o: Id) => boolean
private readonly _commutative: boolean
/**
* 区间修改,单点查询的线段树.
* @param n 线段树的大小.
* @param id 单位元.
* @param composition 父结点`f`与子结点`g`的结合函数.
* @param equals 判断两个值是否相等的函数.比较方式默认为`===`.
* @param commutative 群的结合是否可交换顺序.默认为`false`.为'true'时可以加速区间修改.
*
* @alias DualSegmentTree
*/
constructor(
n: number,
id: () => Id,
composition: (f: Id, g: Id) => Id,
equals: (a: Id, b: Id) => boolean = (a, b) => a === b,
commutative = false
) {
if (!equals(id(), id())) {
throw new Error('equals must be provided when id() returns an non-primitive value')
}
let size = 1
let height = 0
while (size < n) {
size <<= 1
height++
}
const lazy = Array(size << 1)
for (let i = 0; i < lazy.length; i++) lazy[i] = id()
this._n = n
this._size = size
this._height = height
this._lazy = lazy
this._id = id
this._composition = composition
const identity = id()
this._equalsToId = equals ? (o: Id) => equals(o, identity) : (o: Id) => o === identity
this._commutative = commutative
}
get(index: number): Id {
if (index < 0 || index >= this._n) return this._id()
index += this._size
for (let i = this._height; i > 0; i--) this._propagate(index >> i)
return this._lazy[index]
}
/**
* 将区间`[left, right)`的值与`lazy`作用.
*/
update(start: number, end: number, lazy: Id): void {
if (start < 0) start = 0
if (end > this._n) end = this._n
if (start >= end) return
start += this._size
end += this._size
if (!this._commutative) {
for (let i = this._height; i > 0; i--) {
if ((start >> i) << i !== start) this._propagate(start >> i)
if ((end >> i) << i !== end) this._propagate((end - 1) >> i)
}
}
while (start < end) {
if (start & 1) {
this._lazy[start] = this._composition(lazy, this._lazy[start])
start++
}
if (end & 1) {
end--
this._lazy[end] = this._composition(lazy, this._lazy[end])
}
start >>= 1
end >>= 1
}
}
toString(): string {
const sb: string[] = []
sb.push('SegmentTreeRangeUpdatePointGet(')
for (let i = 0; i < this._size; i++) {
this._propagate(i)
}
for (let i = this._size; i < this._size + this._n; i++) {
if (i !== this._size) sb.push(',')
sb.push(String(this._lazy[i]))
}
sb.push(')')
return sb.join('')
}
private _propagate(k: number): void {
if (this._equalsToId(this._lazy[k])) return
this._lazy[k << 1] = this._composition(this._lazy[k], this._lazy[k << 1])
this._lazy[(k << 1) | 1] = this._composition(this._lazy[k], this._lazy[(k << 1) | 1])
this._lazy[k] = this._id()
}
}典型题目:
1622. 奇妙序列
const BIGMOD = BigInt(1e9 + 7)
class Fancy {
private readonly _seg: SegmentTreeRangeUpdatePointGet<[mul: bigint, add: bigint]> =
new SegmentTreeRangeUpdatePointGet(
1e5 + 10,
() => [1n, 0n],
(f, g) => [(f[0] * g[0]) % BIGMOD, (f[0] * g[1] + f[1]) % BIGMOD],
(a, b) => a[0] === b[0] && a[1] === b[1]
)
private _length = 0
append(val: number): void {
this._seg.update(this._length, this._length + 1, [1n, BigInt(val)])
this._length++
}
addAll(inc: number): void {
this._seg.update(0, this._length, [1n, BigInt(inc)])
}
multAll(m: number): void {
this._seg.update(0, this._length, [BigInt(m), 0n])
}
getIndex(idx: number): number {
if (idx >= this._length) return -1
return Number(this._seg.get(idx)[1])
}
}3.区间修改区间查询
SegmentTreeRangeUpdateRangeQuery
class SegmentTreeRangeUpdateRangeQuery<E = number, Id = number> {
private readonly _n: number
private readonly _size: number
private readonly _height: number
private readonly _data: E[]
private readonly _lazy: Id[]
private readonly _e: () => E
private readonly _id: () => Id
private readonly _op: (a: E, b: E) => E
private readonly _mapping: (id: Id, data: E) => E
private readonly _composition: (id1: Id, id2: Id) => Id
private readonly _equalsToId: (o: Id) => boolean
/**
* 区间修改区间查询的懒标记线段树.维护幺半群.
* @param nOrLeaves 大小或叶子节点的值.
* @param operations 线段树的操作.
*/
constructor(
nOrLeaves: number | ArrayLike<E>,
operations: {
/**
* 线段树维护的值的幺元.
*/
e: () => E
/**
* 更新操作/懒标记的幺元.
*/
id: () => Id
/**
* 合并左右区间的值.
*/
op: (e1: E, e2: E) => E
/**
* 父结点的懒标记更新子结点的值.
*/
mapping: (lazy: Id, data: E) => E
/**
* 父结点的懒标记更新子结点的懒标记(合并).
*/
composition: (f: Id, g: Id) => Id
/**
* 判断两个懒标记是否相等.比较方式默认为`===`.
*/
equalsId?: (id1: Id, id2: Id) => boolean
} & ThisType<void>
) {
const n = typeof nOrLeaves === 'number' ? nOrLeaves : nOrLeaves.length
const { e, id, op, mapping, composition, equalsId } = operations
if (!equalsId && !SegmentTreeRangeUpdateRangeQuery._isPrimitive(id())) {
throw new Error('equalsId must be provided when id() returns an non-primitive value')
}
let size = 1
let height = 0
while (size < n) {
size <<= 1
height++
}
const data = Array(size << 1)
for (let i = 0; i < data.length; i++) data[i] = e()
const lazy = Array(size)
for (let i = 0; i < lazy.length; i++) lazy[i] = id()
this._n = n
this._size = size
this._height = height
this._data = data
this._lazy = lazy
this._e = e
this._id = id
this._op = op
this._mapping = mapping
this._composition = composition
const identity = id()
this._equalsToId = equalsId ? (o: Id) => equalsId(o, identity) : (o: Id) => o === identity
if (typeof nOrLeaves !== 'number') this.build(nOrLeaves)
}
set(index: number, value: E): void {
if (index < 0 || index >= this._n) return
index += this._size
for (let i = this._height; i > 0; i--) this._pushDown(index >> i)
this._data[index] = value
for (let i = 1; i <= this._height; i++) this._pushUp(index >> i)
}
get(index: number): E {
if (index < 0 || index >= this._n) return this._e()
index += this._size
for (let i = this._height; i > 0; i--) this._pushDown(index >> i)
return this._data[index]
}
/**
* 区间`[start,end)`的值与`lazy`进行作用.
* 0 <= start <= end <= n.
*/
update(start: number, end: number, lazy: Id): void {
if (start < 0) start = 0
if (end > this._n) end = this._n
if (start >= end) return
start += this._size
end += this._size
for (let i = this._height; i > 0; i--) {
if ((start >> i) << i !== start) this._pushDown(start >> i)
if ((end >> i) << i !== end) this._pushDown((end - 1) >> i)
}
let start2 = start
let end2 = end
for (; start < end; start >>= 1, end >>= 1) {
if (start & 1) this._propagate(start++, lazy)
if (end & 1) this._propagate(--end, lazy)
}
start = start2
end = end2
for (let i = 1; i <= this._height; i++) {
if ((start >> i) << i !== start) this._pushUp(start >> i)
if ((end >> i) << i !== end) this._pushUp((end - 1) >> i)
}
}
/**
* 查询区间`[start,end)`的聚合值.
* 0 <= start <= end <= n.
*/
query(start: number, end: number): E {
if (start < 0) start = 0
if (end > this._n) end = this._n
if (start >= end) return this._e()
start += this._size
end += this._size
for (let i = this._height; i > 0; i--) {
if ((start >> i) << i !== start) this._pushDown(start >> i)
if ((end >> i) << i !== end) this._pushDown((end - 1) >> i)
}
let leftRes = this._e()
let rightRes = this._e()
for (; start < end; start >>= 1, end >>= 1) {
if (start & 1) leftRes = this._op(leftRes, this._data[start++])
if (end & 1) rightRes = this._op(this._data[--end], rightRes)
}
return this._op(leftRes, rightRes)
}
queryAll(): E {
return this._data[1]
}
/**
* 树上二分查询最大的`end`使得`[start,end)`内的值满足`predicate`.
* @alias findFirst
*/
maxRight(start: number, predicate: (value: E) => boolean): number {
if (start < 0) start = 0
if (start >= this._n) return this._n
start += this._size
for (let i = this._height; i > 0; i--) this._pushDown(start >> i)
let res = this._e()
while (true) {
while (!(start & 1)) start >>= 1
if (!predicate(this._op(res, this._data[start]))) {
while (start < this._size) {
this._pushDown(start)
start <<= 1
if (predicate(this._op(res, this._data[start]))) {
res = this._op(res, this._data[start])
start++
}
}
return start - this._size
}
res = this._op(res, this._data[start])
start++
if ((start & -start) === start) break
}
return this._n
}
/**
* 树上二分查询最小的`start`使得`[start,end)`内的值满足`predicate`
* @alias findLast
*/
minLeft(end: number, predicate: (value: E) => boolean): number {
if (end > this._n) end = this._n
if (end <= 0) return 0
end += this._size
for (let i = this._height; i > 0; i--) this._pushDown((end - 1) >> i)
let res = this._e()
while (true) {
end--
while (end > 1 && end & 1) end >>= 1
if (!predicate(this._op(this._data[end], res))) {
while (end < this._size) {
this._pushDown(end)
end = (end << 1) | 1
if (predicate(this._op(this._data[end], res))) {
res = this._op(this._data[end], res)
end--
}
}
return end + 1 - this._size
}
res = this._op(this._data[end], res)
if ((end & -end) === end) break
}
return 0
}
build(leaves: ArrayLike<E>): void {
if (leaves.length !== this._n) throw new RangeError(`length must be equal to ${this._n}`)
for (let i = 0; i < this._n; i++) this._data[this._size + i] = leaves[i]
for (let i = this._size - 1; i > 0; i--) this._pushUp(i)
}
toString(): string {
const sb: string[] = []
sb.push('SegmentTreeRangeUpdateRangeQuery(')
for (let i = 0; i < this._n; i++) {
if (i) sb.push(', ')
sb.push(String(this.get(i)))
}
sb.push(')')
return sb.join('')
}
private _pushUp(index: number): void {
this._data[index] = this._op(this._data[index << 1], this._data[(index << 1) | 1])
}
private _pushDown(index: number): void {
const lazy = this._lazy[index]
if (this._equalsToId(lazy)) return
this._propagate(index << 1, lazy)
this._propagate((index << 1) | 1, lazy)
this._lazy[index] = this._id()
}
private _propagate(index: number, lazy: Id): void {
this._data[index] = this._mapping(lazy, this._data[index])
if (index < this._size) this._lazy[index] = this._composition(lazy, this._lazy[index])
}
private static _isPrimitive(
o: unknown
): o is number | string | boolean | symbol | bigint | null | undefined {
return o === null || (typeof o !== 'object' && typeof o !== 'function')
}
}典型题目:
1622. 奇妙序列
2286. 以组为单位订音乐会的门票
const BIGMOD = BigInt(1e9 + 7)
class Fancy {
private readonly _seg = new SegmentTreeRangeUpdateRangeQuery<
[size: bigint, sum: bigint],
[mul: bigint, add: bigint]
>(1e5 + 10, {
e() {
return [1n, 0n]
},
id() {
return [1n, 0n]
},
op(e1, e2) {
return [e1[0] + e2[0], (e1[1] + e2[1]) % BIGMOD]
},
mapping(lazy, data) {
return [data[0], (data[1] * lazy[0] + data[0] * lazy[1]) % BIGMOD]
},
composition(f, g) {
return [(f[0] * g[0]) % BIGMOD, (f[0] * g[1] + f[1]) % BIGMOD]
},
equalsId(id1, id2) {
return id1[0] === id2[0] && id1[1] === id2[1]
}
})
private _length = 0
append(val: number): void {
this._seg.update(this._length, this._length + 1, [1n, BigInt(val)])
this._length++
}
addAll(inc: number): void {
this._seg.update(0, this._length, [1n, BigInt(inc)])
}
multAll(m: number): void {
this._seg.update(0, this._length, [BigInt(m), 0n])
}
getIndex(idx: number): number {
if (idx >= this._length) return -1
return Number(this._seg.get(idx)[1])
}
}4.二维单点修改区间查询
SegmentTree2DPointUpdateRangeQuery
/**
* 单点修改,区间查询的二维线段树.
*/
class SegmentTree2DPointUpdateRangeQuery<E> {
private readonly _row: number
private readonly _col: number
private readonly _tree: E[]
private readonly _e: () => E
private readonly _op: (a: E, b: E) => E
constructor(row: number, col: number, e: () => E, op: (a: E, b: E) => E) {
this._row = 1
while (this._row < row) this._row <<= 1
this._col = 1
while (this._col < col) this._col <<= 1
this._tree = Array((this._row * this._col) << 2)
for (let i = 0; i < this._tree.length; i++) this._tree[i] = e()
this._e = e
this._op = op
}
/**
* 在 {@link build} 之前调用,设置初始值.
* 0 <= row < ROW, 0 <= col < COL.
*/
addPoint(row: number, col: number, value: E): void {
this._tree[this._id(row + this._row, col + this._col)] = value
}
/**
* 如果调用了 {@link addPoint} 初始化,则需要调用此方法构建树.
*/
build(): void {
for (let c = this._col; c < this._col << 1; c++) {
for (let r = this._row - 1; ~r; r--) {
this._tree[this._id(r, c)] = this._op(
this._tree[this._id(r << 1, c)],
this._tree[this._id((r << 1) | 1, c)]
)
}
}
for (let r = 0; r < this._row << 1; r++) {
for (let c = this._col - 1; ~c; c--) {
this._tree[this._id(r, c)] = this._op(
this._tree[this._id(r, c << 1)],
this._tree[this._id(r, (c << 1) | 1)]
)
}
}
}
/** 0 <= row < ROW, 0 <= col < COL. */
get(row: number, col: number): E {
return this._tree[this._id(row + this._row, col + this._col)]
}
/** 0 <= row < ROW, 0 <= col < COL. */
set(row: number, col: number, target: E): void {
let r = row + this._row
let c = col + this._col
this._tree[this._id(r, c)] = target
for (let i = r >>> 1; i; i >>>= 1) {
this._tree[this._id(i, c)] = this._op(
this._tree[this._id(i << 1, c)],
this._tree[this._id((i << 1) | 1, c)]
)
}
for (; r; r >>>= 1) {
for (let j = c >>> 1; j; j >>>= 1) {
this._tree[this._id(r, j)] = this._op(
this._tree[this._id(r, j << 1)],
this._tree[this._id(r, (j << 1) | 1)]
)
}
}
}
/**
* 查询区间 `[row1, row2)` x `[col1, col2)` 的聚合值.
* 0 <= row1 <= row2 <= ROW.
* 0 <= col1 <= col2 <= COL.
*/
query(row1: number, row2: number, col1: number, col2: number): E {
if (row1 >= row2 || col1 >= col2) return this._e()
let res = this._e()
row1 += this._row
row2 += this._row
col1 += this._col
col2 += this._col
for (; row1 < row2; row1 >>>= 1, row2 >>>= 1) {
if (row1 & 1) {
res = this._op(res, this._query(row1, col1, col2))
row1++
}
if (row2 & 1) {
row2--
res = this._op(res, this._query(row2, col1, col2))
}
}
return res
}
private _id(r: number, c: number): number {
return ((r * this._col) << 1) + c
}
private _query(r: number, c1: number, c2: number): E {
let res = this._e()
for (; c1 < c2; c1 >>>= 1, c2 >>>= 1) {
if (c1 & 1) {
res = this._op(res, this._tree[this._id(r, c1)])
c1++
}
if (c2 & 1) {
c2--
res = this._op(res, this._tree[this._id(r, c2)])
}
}
return res
}
}典型题目:
308. 二维区域和检索 - 可变
class NumMatrix {
private readonly _ROW: number
private readonly _COL: number
private readonly _tree: SegmentTree2DPointUpdateRangeQuery<number>
constructor(matrix: number[][]) {
this._ROW = matrix.length
this._COL = matrix[0].length
this._tree = new SegmentTree2DPointUpdateRangeQuery(
this._ROW,
this._COL,
() => 0,
(a, b) => a + b
)
for (let r = 0; r < this._ROW; r++) {
for (let c = 0; c < this._COL; c++) {
this._tree.addPoint(r, c, matrix[r][c])
}
}
this._tree.build() // !注意如果set了不要忘记 build
}
update(row: number, col: number, val: number): void {
this._tree.set(row, col, val)
}
sumRegion(row1: number, col1: number, row2: number, col2: number): number {
return this._tree.query(row1, row2 + 1, col1, col2 + 1)
}
}5.二维区间修改单点查询
SegmentTree2DRangeUpdatePointGet
interface IRangeUpdatePointGet1D<E, Id> {
update(start: number, end: number, lazy: Id): void
get(index: number): E
set(index: number, value: E): void
}
/**
* 二维区间更新,单点查询的线段树(树套树).
*/
class SegmentTree2DRangeUpdatePointGet<E = number, Id = number> {
/**
* 存储内层的"树"结构.
*/
private readonly _seg: IRangeUpdatePointGet1D<E, Id>[]
/**
* 合并两个内层"树"的结果.
*/
private readonly _mergeRow: (a: E, b: E) => E
/**
* 初始化内层"树"的函数.
*/
private readonly _init1D: () => IRangeUpdatePointGet1D<E, Id>
/**
* 当列数超过行数时,需要对矩阵进行旋转,将列数控制在根号以下.
*/
private readonly _needRotate: boolean
/**
* 原始矩阵的行数(未经旋转).
*/
private readonly _rawRow: number
private readonly _size: number
/**
* @param row 行数.对时间复杂度贡献为`O(log(row))`.
* @param col 列数.内部树的大小.列数越小,对内部树的时间复杂度要求越低.
* @param createRangeUpdatePointGet1D 初始化内层"树"的函数.入参为内层"树"的大小.
* @param mergeRow 合并两个内层"树"的结果.
*/
constructor(
row: number,
col: number,
createRangeUpdatePointGet1D: (n: number) => IRangeUpdatePointGet1D<E, Id>,
mergeRow: (a: E, b: E) => E
) {
this._rawRow = row
this._needRotate = row < col
if (this._needRotate) {
row ^= col
col ^= row
row ^= col
}
let size = 1
while (size < row) size <<= 1
this._seg = Array(2 * size - 1)
this._mergeRow = mergeRow
this._init1D = () => createRangeUpdatePointGet1D(col)
this._size = size
}
/**
* 将`[row1,row2)`x`[col1,col2)`的区间值与`lazy`作用.
*/
update(row1: number, row2: number, col1: number, col2: number, lazy: Id): void {
if (this._needRotate) {
const tmp1 = row1
const tmp2 = row2
row1 = col1
row2 = col2
col1 = this._rawRow - tmp2
col2 = this._rawRow - tmp1
}
this._update(row1, row2, col1, col2, lazy, 0, 0, this._size)
}
get(row: number, col: number): E {
if (this._needRotate) {
const tmp = row
row = col
col = this._rawRow - tmp - 1
}
row += this._size - 1
if (!this._seg[row]) this._seg[row] = this._init1D()
let res = this._seg[row].get(col)
while (row > 0) {
row = (row - 1) >> 1
if (this._seg[row]) res = this._mergeRow(res, this._seg[row].get(col))
}
return res
}
set(row: number, col: number, value: E): void {
if (this._needRotate) {
const tmp = row
row = col
col = this._rawRow - tmp - 1
}
row += this._size - 1
if (!this._seg[row]) this._seg[row] = this._init1D()
this._seg[row].set(col, value)
while (row > 0) {
row = (row - 1) >> 1
if (!this._seg[row]) this._seg[row] = this._init1D()
this._seg[row].set(col, value)
}
}
private _update(
R: number,
C: number,
start: number,
end: number,
lazy: Id,
pos: number,
r: number,
c: number
): void {
if (c <= R || C <= r) return
if (R <= r && c <= C) {
if (!this._seg[pos]) this._seg[pos] = this._init1D()
this._seg[pos].update(start, end, lazy)
} else {
const mid = (r + c) >>> 1
this._update(R, C, start, end, lazy, 2 * pos + 1, r, mid)
this._update(R, C, start, end, lazy, 2 * pos + 2, mid, c)
}
}
}典型题目:
1476. 子矩形查询
2536. 子矩阵元素加 1
/**
* !区间染色,单点求值的线段树.
*/
class SubrectangleQueries {
private _seg2d: SegmentTree2DRangeUpdatePointGet<E, Id>
private _updateTime = 1
constructor(rectangle: ArrayLike<ArrayLike<number>>) {
const row = rectangle.length
const col = rectangle[0].length
const seg2d = new SegmentTree2DRangeUpdatePointGet<E, Id>(
row,
col,
n => new NaiveTree(n),
(a, b) => (a[0] > b[0] ? a : b)
)
this._seg2d = seg2d
for (let i = 0; i < row; ++i) {
const cache = rectangle[i]
for (let j = 0; j < col; ++j) {
this.updateSubrectangle(i, j, i, j, cache[j])
}
}
}
/**
* 将左上角为`[row1, col1]`,右下角为`[row2, col2]`的子矩形中的所有元素更新为`newValue`.
*/
updateSubrectangle(
row1: number,
col1: number,
row2: number,
col2: number,
newValue: number
): void {
this._seg2d.update(row1, row2 + 1, col1, col2 + 1, [this._updateTime++, newValue])
}
getValue(row: number, col: number): number {
return this._seg2d.get(row, col)![1]
}
}
type E = [time: number, value: number]
type Id = E
/**
* 内层"树"的实现.
* 这里把Id拆成两个类型数组存,节省空间.
* 也可以不初始化数组,动态开点.
*/
class NaiveTree {
private readonly _time: Int32Array
private readonly _value: Uint32Array
constructor(n: number) {
this._time = new Int32Array(n)
this._value = new Uint32Array(n)
}
update(start: number, end: number, lazy: Id): void {
this._time.fill(lazy[0], start, end)
this._value.fill(lazy[1], start, end)
}
get(index: number): E {
return [this._time[index], this._value[index]]
}
set(index: number, value: E): void {
this._time[index] = value[0]
this._value[index] = value[1]
}
}6.动态开点单点修改区间查询
SegmentTreeDynamic
type SegNode<E> = {
left: SegNode<E> | undefined
right: SegNode<E> | undefined
index: number
data: E
sum: E
}
class SegmentTreeDynamic<E = number> {
private static _isPrimitive(
o: unknown
): o is number | string | boolean | symbol | bigint | null | undefined {
return o === null || (typeof o !== 'object' && typeof o !== 'function')
}
private readonly _lower: number
private readonly _upper: number
private readonly _e: () => E
private readonly _op: (a: E, b: E) => E
private readonly _persistent: boolean
private _root: SegNode<E>
/**
* 单点修改区间查询的动态开点线段树.线段树维护的值域为`[start, end)`.
* @param start 值域下界.start>=0.
* @param end 值域上界.
* @param e 幺元.
* @param op 结合律的二元操作.
* @param persistent 是否持久化.持久化后,每次修改都会新建一个结点,否则会复用原来的结点.
*/
constructor(start: number, end: number, e: () => E, op: (a: E, b: E) => E, persistent = false) {
if (persistent && !SegmentTreeDynamic._isPrimitive(e())) {
throw new Error('persistent is only supported when e() return primitive values')
}
this._lower = start
this._upper = end + 5
this._e = e
this._op = op
this._persistent = persistent
this._root = this.newRoot()
}
newRoot(): SegNode<E> {
return undefined as any // nil
}
get(index: number, root: SegNode<E> = this._root): E {
if (index < this._lower || index >= this._upper) return this._e()
return this._get(root, index)
}
set(index: number, value: E, root: SegNode<E> = this._root): SegNode<E> {
if (index < this._lower || index >= this._upper) return root
const newRoot = this._set(root, this._lower, this._upper, index, value)
this._root = newRoot
return newRoot
}
update(index: number, value: E, root: SegNode<E> = this._root): SegNode<E> {
if (index < this._lower || index >= this._upper) return root
const newRoot = this._update(root, this._lower, this._upper, index, value)
this._root = newRoot
return newRoot
}
/**
* 查询区间`[start,end)`的聚合值.
* {@link _lower} <= start <= end <= {@link _upper}.
*/
query(start: number, end: number, root: SegNode<E> = this._root): E {
if (start < this._lower) start = this._lower
if (end > this._upper) end = this._upper
if (start >= end) return this._e()
let res = this._e()
const _query = (node: SegNode<E> | undefined, l: number, r: number, ql: number, qr: number) => {
if (!node) return
ql = l > ql ? l : ql
qr = r < qr ? r : qr
if (ql >= qr) return
if (l === ql && r === qr) {
res = this._op(res, node.sum)
return
}
const m = Math.floor(l + (r - l) / 2)
_query(node.left, l, m, ql, qr)
if (ql <= node.index && node.index < qr) {
res = this._op(res, node.data)
}
_query(node.right, m, r, ql, qr)
}
_query(root, this._lower, this._upper, start, end)
return res
}
queryAll(root: SegNode<E> = this._root): E {
return root.sum
}
/**
* 二分查询最大的`end`使得切片`[start:end)`内的聚合值满足`check`.
* {@link _lower} <= start <= {@link _upper}.
* @alias findFirst
*/
maxRight(start: number, check: (e: E) => boolean, root: SegNode<E> = this._root): number {
if (start < this._lower) start = this._lower
if (start >= this._upper) return this._upper
let x = this._e()
const _maxRight = (node: SegNode<E> | undefined, l: number, r: number, ql: number): number => {
if (!node || r <= ql) return this._upper
const tmp = this._op(x, node.sum)
if (check(tmp)) {
x = tmp
return this._upper
}
const m = Math.floor(l + (r - l) / 2)
const k = _maxRight(node.left, l, m, ql)
if (k !== this._upper) return k
if (ql <= node.index) {
x = this._op(x, node.data)
if (!check(x)) {
return node.index
}
}
return _maxRight(node.right, m, r, ql)
}
return _maxRight(root, this._lower, this._upper, start)
}
/**
* 二分查询最小的`start`使得切片`[start:end)`内的聚合值满足`check`.
* {@link _lower} <= end <= {@link _upper}.
* @alias findLast
*/
minLeft(end: number, check: (e: E) => boolean, root: SegNode<E> = this._root): number {
if (end > this._upper) end = this._upper
if (end <= this._lower) return this._lower
let x = this._e()
const _minLeft = (node: SegNode<E> | undefined, l: number, r: number, qr: number): number => {
if (!node || qr <= l) return this._lower
const tmp = this._op(node.sum, x)
if (check(tmp)) {
x = tmp
return this._lower
}
const m = Math.floor(l + (r - l) / 2)
const k = _minLeft(node.right, m, r, qr)
if (k !== this._lower) return k
if (node.index < qr) {
x = this._op(node.data, x)
if (!check(x)) {
return node.index + 1
}
}
return _minLeft(node.left, l, m, qr)
}
return _minLeft(root, this._lower, this._upper, end)
}
getAll(root: SegNode<E> = this._root): [index: number, value: E][] {
const res: [number, E][] = []
const _getAll = (node: SegNode<E> | undefined) => {
if (!node) return
_getAll(node.left)
res.push([node.index, node.data])
_getAll(node.right)
}
_getAll(root)
return res
}
private _copyNode(node: SegNode<E>): SegNode<E> {
if (!node || !this._persistent) return node
return { left: node.left, right: node.right, index: node.index, data: node.data, sum: node.sum }
}
private _get(root: SegNode<E> | undefined, index: number): E {
if (!root) return this._e()
if (index === root.index) return root.data
if (index < root.index) return this._get(root.left, index)
return this._get(root.right, index)
}
private _set(root: SegNode<E> | undefined, l: number, r: number, i: number, x: E): SegNode<E> {
if (!root) return SegmentTreeDynamic._newNode(i, x)
root = this._copyNode(root)
if (root.index === i) {
root.data = x
this._pushUp(root)
return root
}
const m = Math.floor(l + (r - l) / 2)
if (i < m) {
if (root.index < i) {
const tmp1 = root.index
root.index = i
i = tmp1
const tmp2 = root.data
root.data = x
x = tmp2
}
root.left = this._set(root.left, l, m, i, x)
} else {
if (i < root.index) {
const tmp1 = root.index
root.index = i
i = tmp1
const tmp2 = root.data
root.data = x
x = tmp2
}
root.right = this._set(root.right, m, r, i, x)
}
this._pushUp(root)
return root
}
private _pushUp(root: SegNode<E>): void {
root.sum = root.data
if (root.left) root.sum = this._op(root.left.sum, root.sum)
if (root.right) root.sum = this._op(root.sum, root.right.sum)
}
private _update(root: SegNode<E> | undefined, l: number, r: number, i: number, x: E): SegNode<E> {
if (!root) return SegmentTreeDynamic._newNode(i, x)
root = this._copyNode(root)
if (root.index === i) {
root.data = this._op(root.data, x)
this._pushUp(root)
return root
}
const m = Math.floor(l + (r - l) / 2)
if (i < m) {
if (root.index < i) {
const tmp1 = root.index
root.index = i
i = tmp1
const tmp2 = root.data
root.data = x
x = tmp2
}
root.left = this._update(root.left, l, m, i, x)
} else {
if (i < root.index) {
const tmp1 = root.index
root.index = i
i = tmp1
const tmp2 = root.data
root.data = x
x = tmp2
}
root.right = this._update(root.right, m, r, i, x)
}
this._pushUp(root)
return root
}
private static _newNode<V>(index: number, value: V): SegNode<V> {
return {
index,
left: undefined,
right: undefined,
data: value,
sum: value
}
}
}典型题目:
2736. 最大和查询
function maximumSumQueries(nums1: number[], nums2: number[], queries: number[][]): number[] {
const points = nums1.map((v, i) => [v, nums2[i]]).sort((a, b) => a[0] - b[0] || a[1] - b[1])
const qWithId = queries.map((q, i) => [q[0], q[1], i]).sort((a, b) => a[0] - b[0] || a[1] - b[1])
const seg = new SegmentTreeDynamic<number>(0, 1e9 + 10, () => -INF, Math.max)
const res = Array(queries.length).fill(-1)
let pi = points.length - 1
for (let i = qWithId.length - 1; i >= 0; i--) {
const [qx, qy, qid] = qWithId[i]
while (pi >= 0 && points[pi][0] >= qx) {
seg.update(points[pi][1]!, points[pi][0] + points[pi][1])
pi--
}
const curMax = seg.query(qy!, 1e9 + 10)
res[qid] = curMax === -INF ? -1 : curMax
}
return res
}7.动态开点区间修改区间查询
SegmentTreeDynamicLazy
type SegNode<E, Id> = {
left: SegNode<E, Id> | undefined
right: SegNode<E, Id> | undefined
data: E
id: Id
}
class SegmentTreeDynamicLazy<E = number, Id = number> {
private static _isPrimitive(
o: unknown
): o is number | string | boolean | symbol | bigint | null | undefined {
return o === null || (typeof o !== 'object' && typeof o !== 'function')
}
private readonly _lower: number
private readonly _upper: number
private readonly _e: () => E
private readonly _eRange: (start: number, end: number) => E
private readonly _id: () => Id
private readonly _op: (a: E, b: E) => E
private readonly _mapping: (id: Id, data: E, size: number) => E
private readonly _composition: (id1: Id, id2: Id) => Id
private readonly _equalsToId: (o: Id) => boolean
private readonly _persistent: boolean
private _root: SegNode<E, Id>
/**
* 区间修改区间查询的动态开点懒标记线段树.线段树维护的值域为`[start, end)`.
* @param start 值域下界.start>=0.
* @param end 值域上界.
* @param operations 线段树的操作.
* @param persistent 是否持久化.持久化后,每次修改都会新建一个结点,否则会复用原来的结点.
* @alias NodeManager
*/
constructor(
start: number,
end: number,
operations: {
/**
* 线段树维护的值的幺元.
*/
e: () => E
/**
* 结点的初始值.用于维护结点的范围.
*/
eRange?: (start: number, end: number) => E
/**
* 更新操作/懒标记的幺元.
*/
id: () => Id
/**
* 合并左右区间的值.
*/
op: (e1: E, e2: E) => E
/**
* 父结点的懒标记更新子结点的值.
*/
mapping: (lazy: Id, data: E, size: number) => E
/**
* 父结点的懒标记更新子结点的懒标记(合并).
*/
composition: (f: Id, g: Id) => Id
/**
* 判断两个懒标记是否相等.比较方式默认为`===`.
*/
equalsId?: (id1: Id, id2: Id) => boolean
} & ThisType<void>,
persistent = false
) {
const { e, eRange, id, op, mapping, composition, equalsId } = operations
if (!equalsId && !SegmentTreeDynamicLazy._isPrimitive(id())) {
throw new Error('equalsId must be provided when id() returns an non-primitive value')
}
if (
persistent &&
!(SegmentTreeDynamicLazy._isPrimitive(e()) && SegmentTreeDynamicLazy._isPrimitive(id()))
) {
throw new Error('persistent is only supported when e() and id() return primitive values')
}
this._lower = start
this._upper = end + 5
this._e = e
this._eRange = eRange || e
this._id = id
this._op = op
this._mapping = mapping
this._composition = composition
const identity = id()
this._equalsToId = equalsId ? (o: Id) => equalsId(o, identity) : (o: Id) => o === identity
this._persistent = persistent
this._root = this.newRoot()
}
newRoot(): SegNode<E, Id> {
return {
left: undefined,
right: undefined,
data: this._eRange(this._lower, this._upper),
id: this._id()
}
}
build(leaves: ArrayLike<E>): SegNode<E, Id> {
const newRoot = this._build(0, leaves.length, leaves)!
this._root = newRoot
return newRoot
}
get(index: number, root: SegNode<E, Id> = this._root): E {
return this.query(index, index + 1, root)
}
set(index: number, value: E, root: SegNode<E, Id> = this._root): SegNode<E, Id> {
if (index < this._lower || index >= this._upper) return root
const newRoot = this._set(root, this._lower, this._upper, index, value)
this._root = newRoot
return newRoot
}
update(index: number, value: E, root: SegNode<E, Id> = this._root): SegNode<E, Id> {
if (index < this._lower || index >= this._upper) return root
const newRoot = this._update(root, this._lower, this._upper, index, value)
this._root = newRoot
return newRoot
}
/**
* 区间`[start,end)`的值与`lazy`进行作用.
* {@link _lower} <= start <= end <= {@link _upper}.
*/
updateRange(
start: number,
end: number,
lazy: Id,
root: SegNode<E, Id> = this._root
): SegNode<E, Id> {
if (start < this._lower) start = this._lower
if (end > this._upper) end = this._upper
if (start >= end) return root
const newRoot = this._updateRange(root, this._lower, this._upper, start, end, lazy)
this._root = newRoot
return newRoot
}
/**
* 查询区间`[start,end)`的聚合值.
* {@link _lower} <= start <= end <= {@link _upper}.
*/
query(start: number, end: number, root: SegNode<E, Id> = this._root): E {
if (start < this._lower) start = this._lower
if (end > this._upper) end = this._upper
if (start >= end) return this._e()
let res = this._e()
const _query = (
node: SegNode<E, Id> | undefined,
l: number,
r: number,
ql: number,
qr: number,
lazy: Id
) => {
ql = l > ql ? l : ql
qr = r < qr ? r : qr
if (ql >= qr) return
if (!node) {
res = this._op(res, this._mapping(lazy, this._eRange(ql, qr), qr - ql))
return
}
if (l === ql && r === qr) {
res = this._op(res, this._mapping(lazy, node.data, r - l))
return
}
const mid = Math.floor(l + (r - l) / 2)
lazy = this._composition(lazy, node.id)
_query(node.left, l, mid, ql, qr, lazy)
_query(node.right, mid, r, ql, qr, lazy)
}
_query(root, this._lower, this._upper, start, end, this._id())
return res
}
queryAll(root: SegNode<E, Id> = this._root): E {
return root.data
}
/**
* 二分查询最大的`end`使得切片`[start:end)`内的聚合值满足`check`.
* {@link _lower} <= start <= {@link _upper}.
* @alias findFirst
*/
maxRight(start: number, check: (e: E) => boolean, root: SegNode<E, Id> = this._root): number {
if (start < this._lower) start = this._lower
if (start >= this._upper) return this._upper
let x = this._e()
const _maxRight = (
node: SegNode<E, Id> | undefined,
l: number,
r: number,
ql: number
): number => {
if (r <= ql) return r
if (!node) node = this._newNode(l, r)
ql = l > ql ? l : ql
if (l === ql) {
const tmp = this._op(x, node.data)
if (check(tmp)) {
x = tmp
return r
}
}
if (r === l + 1) return l
this._pushDown(node, l, r)
const m = Math.floor(l + (r - l) / 2)
const k = _maxRight(node.left, l, m, ql)
if (m > k) return k
return _maxRight(node.right, m, r, ql)
}
return _maxRight(root, this._lower, this._upper, start)
}
/**
* 二分查询最小的`start`使得切片`[start:end)`内的聚合值满足`check`.
* {@link _lower} <= end <= {@link _upper}.
* @alias findLast
*/
minLeft(end: number, check: (e: E) => boolean, root: SegNode<E, Id> = this._root): number {
if (end > this._upper) end = this._upper
if (end <= this._lower) return this._lower
let x = this._e()
const _minLeft = (
node: SegNode<E, Id> | undefined,
l: number,
r: number,
qr: number
): number => {
if (qr <= l) return l
if (!node) node = this._newNode(l, r)
qr = r < qr ? r : qr
if (r === qr) {
const tmp = this._op(node.data, x)
if (check(tmp)) {
x = tmp
return l
}
}
if (r === l + 1) return r
this._pushDown(node, l, r)
const m = Math.floor(l + (r - l) / 2)
const k = _minLeft(node.right, m, r, qr)
if (m < k) return k
return _minLeft(node.left, l, m, qr)
}
return _minLeft(root, this._lower, this._upper, end)
}
/**
* `破坏性`地合并node1和node2.
* @warning Not Verified.
*/
mergeDestructively(node1: SegNode<E, Id>, node2: SegNode<E, Id>): SegNode<E, Id> {
const newRoot = this._merge(node1, node2)
if (!newRoot) throw new Error('merge failed')
return newRoot
}
getAll(root: SegNode<E, Id> = this._root): E[] {
if (this._upper - this._lower > 1e7) throw new Error('too large')
const res: E[] = []
const _getAll = (node: SegNode<E, Id> | undefined, l: number, r: number, lazy: Id) => {
if (!node) node = this._newNode(l, r)
if (r - l === 1) {
res.push(this._mapping(lazy, node.data, 1))
return
}
const m = Math.floor(l + (r - l) / 2)
lazy = this._composition(lazy, node.id)
_getAll(node.left, l, m, lazy)
_getAll(node.right, m, r, lazy)
}
_getAll(root, this._lower, this._upper, this._id())
return res
}
private _copyNode(node: SegNode<E, Id>): SegNode<E, Id> {
if (!node || !this._persistent) return node
// TODO: 如果是引用类型, 持久化时需要深拷贝
// !不要使用`...`,很慢
return { left: node.left, right: node.right, data: node.data, id: node.id }
}
private _set(root: SegNode<E, Id>, l: number, r: number, i: number, x: E): SegNode<E, Id> {
if (l === r - 1) {
root = this._copyNode(root)
root.data = x
root.id = this._id()
return root
}
this._pushDown(root, l, r)
const m = Math.floor(l + (r - l) / 2)
if (!root.left) root.left = this._newNode(l, m)
if (!root.right) root.right = this._newNode(m, r)
root = this._copyNode(root)
if (i < m) {
root.left = this._set(root.left!, l, m, i, x)
} else {
root.right = this._set(root.right!, m, r, i, x)
}
root.data = this._op(root.left!.data, root.right!.data)
return root
}
private _update(root: SegNode<E, Id>, l: number, r: number, i: number, x: E): SegNode<E, Id> {
if (l === r - 1) {
root = this._copyNode(root)
root.data = this._op(root.data, x)
root.id = this._id()
return root
}
this._pushDown(root, l, r)
const m = Math.floor(l + (r - l) / 2)
if (!root.left) root.left = this._newNode(l, m)
if (!root.right) root.right = this._newNode(m, r)
root = this._copyNode(root)
if (i < m) {
root.left = this._update(root.left!, l, m, i, x)
} else {
root.right = this._update(root.right!, m, r, i, x)
}
root.data = this._op(root.left!.data, root.right!.data)
return root
}
private _updateRange(
root: SegNode<E, Id> | undefined,
l: number,
r: number,
ql: number,
qr: number,
lazy: Id
): SegNode<E, Id> {
if (!root) root = this._newNode(l, r)
ql = l > ql ? l : ql
qr = r < qr ? r : qr
if (ql >= qr) return root
if (l === ql && r === qr) {
root = this._copyNode(root)
root.data = this._mapping(lazy, root.data, r - l)
root.id = this._composition(lazy, root.id)
return root
}
this._pushDown(root, l, r)
const m = Math.floor(l + (r - l) / 2)
root = this._copyNode(root)
root.left = this._updateRange(root.left, l, m, ql, qr, lazy)
root.right = this._updateRange(root.right, m, r, ql, qr, lazy)
root.data = this._op(root.left!.data, root.right!.data)
return root
}
private _pushDown(node: SegNode<E, Id>, l: number, r: number): void {
const lazy = node.id
if (this._equalsToId(lazy)) return
const m = Math.floor(l + (r - l) / 2)
if (!node.left) {
node.left = this._newNode(l, m)
} else {
node.left = this._copyNode(node.left)
}
const leftChild = node.left!
leftChild.data = this._mapping(lazy, leftChild.data, m - l)
leftChild.id = this._composition(lazy, leftChild.id)
if (!node.right) {
node.right = this._newNode(m, r)
} else {
node.right = this._copyNode(node.right)
}
const rightChild = node.right!
rightChild.data = this._mapping(lazy, rightChild.data, r - m)
rightChild.id = this._composition(lazy, rightChild.id)
node.id = this._id()
}
private _newNode(l: number, r: number): SegNode<E, Id> {
return { left: undefined, right: undefined, data: this._eRange(l, r), id: this._id() }
}
private _build(left: number, right: number, nums: ArrayLike<E>): SegNode<E, Id> | undefined {
if (left === right) return undefined
if (right === left + 1) {
return { left: undefined, right: undefined, data: nums[left], id: this._id() }
}
const m = (left + right) >>> 1
const lRoot = this._build(left, m, nums)
const rRoot = this._build(m, right, nums)
return { left: lRoot, right: rRoot, data: this._op(lRoot!.data, rRoot!.data), id: this._id() }
}
private _merge(
node1: SegNode<E, Id> | undefined,
node2: SegNode<E, Id> | undefined
): SegNode<E, Id> | undefined {
if (!node1 || !node2) return node1 || node2
node1.left = this._merge(node1.left, node2.left)
node1.right = this._merge(node1.right, node2.right)
// pushUp
const left = node1.left
const right = node1.right
node1.data = this._op(left ? left.data : this._e(), right ? right.data : this._e())
return node1
}
}典型题目:
699. 掉落的方块
715. Range 模块
732. 我的日程安排表 III
2271. 毯子覆盖的最多白色砖块数
2276. 统计区间中的整数数目
const INF = 2e15
function fallingSquares(positions: number[][]): number[] {
const res = Array<number>(positions.length).fill(0)
const tree = new SegmentTreeDynamicLazy(0, 2e8 + 10, {
e() {
return 0
},
id() {
return -INF
},
op(x, y) {
return Math.max(x, y)
},
mapping(f, x) {
return f === -INF ? x : Math.max(f, x)
},
composition(f, g) {
return f === -INF ? g : Math.max(f, g)
}
})
positions.forEach(([left, size], i) => {
const right = left + size - 1
const preHeihgt = tree.query(left, right + 1)
tree.updateRange(left, right + 1, preHeihgt + size)
res[i] = tree.queryAll()
})
return res
}8.可持久化线段树
SegmentTreePersistent
type SegNode<E> = {
data: E
left: SegNode<E> | undefined
right: SegNode<E> | undefined
}
class SegmentTreePersistent<E> {
private readonly _e: () => E
private readonly _op: (a: E, b: E) => E
private _size!: number
/**
* 可持久化线段树.支持单点更新,区间查询.
* @param e 单位元.
* @param op 结合律的二元操作.
*/
constructor(e: () => E, op: (a: E, b: E) => E) {
this._e = e
this._op = op
}
build(leaves: ArrayLike<E>): SegNode<E> {
this._size = leaves.length
return this._build(0, this._size, leaves)
}
set(root: SegNode<E>, index: number, value: E): SegNode<E> {
if (index < 0 || index >= this._size) return root
return this._set(root, index, value, 0, this._size)
}
update(root: SegNode<E>, index: number, value: E): SegNode<E> {
if (index < 0 || index >= this._size) return root
return this._update(root, index, value, 0, this._size)
}
query(root: SegNode<E>, start: number, end: number): E {
if (start < 0) start = 0
if (end > this._size) end = this._size
if (start >= end) return this._e()
return this._query(root, start, end, 0, this._size)
}
getAll(root: SegNode<E>): E[] {
const leaves: E[] = Array(this._size)
let ptr = 0
dfs(root)
return leaves
function dfs(cur: SegNode<E> | undefined) {
if (!cur) return
if (!cur.left && !cur.right) {
leaves[ptr++] = cur.data
return
}
dfs(cur.left)
dfs(cur.right)
}
}
private _build(l: number, r: number, leaves: ArrayLike<E>): SegNode<E> {
if (l + 1 >= r) return { data: leaves[l], left: undefined, right: undefined }
const mid = (l + r) >> 1
return this._merge(this._build(l, mid, leaves), this._build(mid, r, leaves))
}
private _merge(l: SegNode<E>, r: SegNode<E>): SegNode<E> {
return { data: this._op(l.data, r.data), left: l, right: r }
}
private _set(root: SegNode<E>, index: number, value: E, l: number, r: number): SegNode<E> {
if (r <= index || index + 1 <= l) return root
if (index <= l && r <= index + 1) return { data: value, left: undefined, right: undefined }
const mid = (l + r) >> 1
return this._merge(
this._set(root.left!, index, value, l, mid),
this._set(root.right!, index, value, mid, r)
)
}
private _update(root: SegNode<E>, index: number, value: E, l: number, r: number): SegNode<E> {
if (r <= index || index + 1 <= l) return root
if (index <= l && r <= index + 1) {
return { data: this._op(root.data, value), left: undefined, right: undefined }
}
const mid = (l + r) >> 1
return this._merge(
this._update(root.left!, index, value, l, mid),
this._update(root.right!, index, value, mid, r)
)
}
private _query(root: SegNode<E>, start: number, end: number, l: number, r: number): E {
if (r <= start || end <= l) return this._e()
if (start <= l && r <= end) return root.data
const mid = (l + r) >> 1
return this._op(
this._query(root.left!, start, end, l, mid),
this._query(root.right!, start, end, mid, r)
)
}
}力扣上没有专门的可持久化线段树的题目,但是下面这道可持久化的题可以用可持久化线段树来做:
典型题目:
1146. 快照数组
class SnapshotArray {
private readonly _seg: SegmentTreePersistent<number>
private readonly _git: SegNode<number>[] = []
private _root: SegNode<number>
constructor(length: number) {
this._seg = new SegmentTreePersistent(
() => -INF,
(a, b) => (a === -INF ? b : a)
)
this._root = this._seg.build(Array(length).fill(0))
}
set(index: number, val: number): void {
this._root = this._seg.set(this._root, index, val)
}
snap(): number {
this._git.push(this._root)
return this._git.length - 1
}
get(index: number, snapId: number): number {
return this._seg.query(this._git[snapId], index, index + 1)
}
}9.01 线段树
SegmentTree01
class SegmentTree01 {
private readonly _n: number
private readonly _ones: Uint32Array
private readonly _lazyFlip: Uint8Array
/**
* little-endian
* @param bitsOrLength 0/1数组或者是长度.注意必须要是正整数.
* @example
* ```ts
* const seg01 = new SegmentTree01([1, 0, 1, 1, 0, 1])
* seg01.toString() // 101101
* ```
*/
constructor(bitsOrLength: ArrayLike<number> | number) {
if (typeof bitsOrLength === 'number') bitsOrLength = Array(bitsOrLength).fill(0)
if (bitsOrLength.length === 0) throw new Error('empty bits')
this._n = bitsOrLength.length
const log = 32 - Math.clz32(this._n - 1)
const size = 1 << log
this._ones = new Uint32Array(size << 1)
this._lazyFlip = new Uint8Array(size) // 叶子结点不需要更新lazy (composition)
this._build(1, 1, this._n, bitsOrLength)
}
/**
* 0 <= start <= end <= n
* 翻转[start,end)区间的bit.
*/
flip(start: number, end: number): void {
if (start < 0) start = 0
if (end > this._n) end = this._n
if (start >= end) return
start++
this._flip(1, start, end, 1, this._n)
}
/**
* 0 <= position <= n-1.
* @param searchDigit 0/1
* @param position 查找的起始位置, 0 <= position < n.
*/
indexOf(searchDigit: 0 | 1, position = 0): number {
position++
if (position > this._n) return -1
if (searchDigit === 0) {
const cand = this._indexofZero(1, position, 1, this._n)
return cand === -1 ? cand : cand - 1
}
const cand = this._indexofOne(1, position, 1, this._n)
return cand === -1 ? cand : cand - 1
}
/**
* 0 <= position <= n-1.
* @param searchDigit 0/1
* @param position 查找的起始位置, 0 <= position < n.
*/
lastIndexOf(searchDigit: 0 | 1, position = this._n - 1): number {
position++
if (position < 1) return -1
if (searchDigit === 0) {
const cand = this._lastIndexOfZero(1, position, 1, this._n)
return cand === -1 ? cand : cand - 1
}
const cand = this._lastIndexOfOne(1, position, 1, this._n)
return cand === -1 ? cand : cand - 1
}
/**
* 0 <= left <= right <= n
* 返回[left,right)区间内1的个数.
*/
onesCount(start: number, end: number): number {
if (start < 0) start = 0
if (end > this._n) end = this._n
if (start >= end) return 0
start++
return this._onesCount(1, start, end, 1, this._n)
}
/**
* 树上二分查询第k个0/1的位置.如果不存在第k个0/1,返回-1.
* !k >= 1
* @returns -1<=pos<n.
*/
kth(searchDigit: 0 | 1, k: number): number {
if (searchDigit === 0) {
if (k > this._n - this._ones[1]) return -1
return this._kthZero(1, k, 1, this._n) - 1
}
if (k > this._ones[1]) return -1
return this._kthOne(1, k, 1, this._n) - 1
}
toString(): string {
const sb: string[] = []
this._toString(1, 1, this._n, sb)
return sb.join('')
}
private _flip(root: number, L: number, R: number, l: number, r: number): void {
if (L <= l && r <= R) {
this._propagateFlip(root, l, r)
return
}
this._pushDown(root, l, r)
const mid = (l + r) >>> 1
if (L <= mid) this._flip(root << 1, L, R, l, mid)
if (mid < R) this._flip((root << 1) | 1, L, R, mid + 1, r)
this._pushUp(root)
}
private _indexofOne(root: number, position: number, left: number, right: number): number {
if (left === right) {
if (this._ones[root] > 0) return left
return -1
}
this._pushDown(root, left, right)
const mid = (left + right) >>> 1
if (position <= mid && this._ones[root << 1] > 0) {
const leftPos = this._indexofOne(root << 1, position, left, mid)
if (leftPos > 0) return leftPos
}
return this._indexofOne((root << 1) | 1, position, mid + 1, right)
}
private _indexofZero(root: number, position: number, left: number, right: number): number {
if (left === right) {
if (this._ones[root] === 0) return left
return -1
}
this._pushDown(root, left, right)
const mid = (left + right) >>> 1
if (position <= mid && this._ones[root << 1] < mid - left + 1) {
const leftPos = this._indexofZero(root << 1, position, left, mid)
if (leftPos > 0) return leftPos
}
return this._indexofZero((root << 1) | 1, position, mid + 1, right)
}
private _lastIndexOfOne(root: number, position: number, left: number, right: number): number {
if (left === right) {
if (this._ones[root] > 0) return left
return -1
}
this._pushDown(root, left, right)
const mid = (left + right) >>> 1
if (position > mid && this._ones[(root << 1) | 1] > 0) {
const rightPos = this._lastIndexOfOne((root << 1) | 1, position, mid + 1, right)
if (rightPos > 0) return rightPos
}
return this._lastIndexOfOne(root << 1, position, left, mid)
}
private _lastIndexOfZero(root: number, position: number, left: number, right: number): number {
if (left === right) {
if (this._ones[root] === 0) return left
return -1
}
this._pushDown(root, left, right)
const mid = (left + right) >>> 1
if (position > mid && this._ones[(root << 1) | 1] < right - mid) {
const rightPos = this._lastIndexOfZero((root << 1) | 1, position, mid + 1, right)
if (rightPos > 0) return rightPos
}
return this._lastIndexOfZero(root << 1, position, left, mid)
}
private _onesCount(root: number, L: number, R: number, l: number, r: number): number {
if (L <= l && r <= R) return this._ones[root]
this._pushDown(root, l, r)
const mid = (l + r) >>> 1
let res = 0
if (L <= mid) res += this._onesCount(root << 1, L, R, l, mid)
if (mid < R) res += this._onesCount((root << 1) | 1, L, R, mid + 1, r)
return res
}
private _kthOne(root: number, k: number, left: number, right: number): number {
if (left === right) return left
this._pushDown(root, left, right)
const mid = (left + right) >>> 1
if (this._ones[root << 1] >= k) return this._kthOne(root << 1, k, left, mid)
return this._kthOne((root << 1) | 1, k - this._ones[root << 1], mid + 1, right)
}
private _kthZero(root: number, k: number, left: number, right: number): number {
if (left === right) return left
this._pushDown(root, left, right)
const mid = (left + right) >>> 1
const leftZero = mid - left + 1 - this._ones[root << 1]
if (leftZero >= k) return this._kthZero(root << 1, k, left, mid)
return this._kthZero((root << 1) | 1, k - leftZero, mid + 1, right)
}
private _toString(root: number, left: number, right: number, sb: string[]): void {
if (left === right) {
sb.push(this._ones[root] === 1 ? '1' : '0')
return
}
this._pushDown(root, left, right)
const mid = (left + right) >>> 1
this._toString(root << 1, left, mid, sb)
this._toString((root << 1) | 1, mid + 1, right, sb)
}
private _build(root: number, left: number, right: number, leaves: ArrayLike<number>): void {
if (left === right) {
this._ones[root] = leaves[left - 1]
return
}
const mid = (left + right) >>> 1
this._build(root << 1, left, mid, leaves)
this._build((root << 1) | 1, mid + 1, right, leaves)
this._pushUp(root)
}
private _pushUp(root: number): void {
this._ones[root] = this._ones[root << 1] + this._ones[(root << 1) | 1]
}
private _pushDown(root: number, left: number, right: number): void {
if (this._lazyFlip[root] !== 0) {
const mid = (left + right) >>> 1
this._propagateFlip(root << 1, left, mid)
this._propagateFlip((root << 1) | 1, mid + 1, right)
this._lazyFlip[root] = 0
}
}
private _propagateFlip(root: number, left: number, right: number): void {
this._ones[root] = right - left + 1 - this._ones[root]
if (root < this._lazyFlip.length) {
this._lazyFlip[root] ^= 1
}
}
}典型题目:
406. 根据身高重建队列
2166. 设计位集
2569. 更新数组后处理求和查询
function reconstructQueue(people: number[][]): number[][] {
const n = people.length
people.sort((a, b) => a[0] - b[0] || -(a[1] - b[1]))
const tree = new SegmentTree01(new Uint8Array(n).fill(1))
const res = Array.from<unknown, [height: number, preCount: number]>({ length: n }, () => [0, 0])
people.forEach(([height, preCount]) => {
const pos = tree.kth(1, preCount + 1)
res[pos] = [height, preCount]
tree.flip(pos, pos + 1)
})
return res
}10.常用的幺半群
SegmentTreeMonoid
const INF = 2e15
/**
* 区间加,查询区间最大值(幺元为0).
*/
function createRangeAddRangeMax(
nOrNums: number | ArrayLike<number>
): SegmentTreeRangeUpdateRangeQuery<number, number> {
return new SegmentTreeRangeUpdateRangeQuery(nOrNums, {
e: () => 0,
id: () => 0,
op: (a, b) => Math.max(a, b),
mapping: (f, x) => f + x,
composition: (f, g) => f + g
})
}
/**
* 区间加,查询区间最小值(幺元为INF).
*/
function createRangeAddRangeMin(
nOrNums: number | ArrayLike<number>
): SegmentTreeRangeUpdateRangeQuery<number, number> {
return new SegmentTreeRangeUpdateRangeQuery(nOrNums, {
e: () => INF,
id: () => 0,
op: (a, b) => Math.min(a, b),
mapping: (f, x) => f + x,
composition: (f, g) => f + g
})
}
/**
* 区间更新最大值,查询区间最大值(幺元为0).
*/
function createRangeUpdateRangeMax(
nOrNums: number | ArrayLike<number>
): SegmentTreeRangeUpdateRangeQuery<number, number> {
return new SegmentTreeRangeUpdateRangeQuery(nOrNums, {
e: () => 0,
id: () => -INF,
op: (a, b) => Math.max(a, b),
mapping: (f, x) => (f === -INF ? x : Math.max(f, x)),
composition: (f, g) => (f === -INF ? g : Math.max(f, g))
})
}
/**
* 区间更新最小值,查询区间最小值(幺元为INF).
*/
function createRangeUpdateRangeMin(
nOrNums: number | ArrayLike<number>
): SegmentTreeRangeUpdateRangeQuery<number, number> {
return new SegmentTreeRangeUpdateRangeQuery(nOrNums, {
e: () => INF,
id: () => INF,
op: (a, b) => Math.min(a, b),
mapping: (f, x) => (f === INF ? x : Math.min(f, x)),
composition: (f, g) => (f === INF ? g : Math.min(f, g))
})
}
/**
* 区间赋值,查询区间和(幺元为0).
*/
function createRangeAssignRangeSum(
nOrNums: number | ArrayLike<[sum: number, size: number]>
): SegmentTreeRangeUpdateRangeQuery<[sum: number, size: number], number> {
return new SegmentTreeRangeUpdateRangeQuery<[sum: number, size: number], number>(nOrNums, {
e: () => [0, 1],
id: () => -1,
op: ([sum1, size1], [sum2, size2]) => [sum1 + sum2, size1 + size2],
mapping: (f, [sum, size]) => (f === -1 ? [sum, size] : [f * size, size]),
composition: (f, g) => (f === -1 ? g : f)
})
}
/**
* 区间赋值,查询区间最大值(幺元为-INF).
*/
function createRangeAssignRangeMax(
nOrNums: number | ArrayLike<number>
): SegmentTreeRangeUpdateRangeQuery<number, number> {
return new SegmentTreeRangeUpdateRangeQuery(nOrNums, {
e: () => 0,
id: () => -INF,
op: (a, b) => Math.max(a, b),
mapping: (f, x) => (f === -INF ? x : f),
composition: (f, g) => (f === -INF ? g : f)
})
}
/**
* 区间赋值,查询区间最小值(幺元为INF).
*/
function createRangeAssignRangeMin(
nOrNums: number | ArrayLike<number>
): SegmentTreeRangeUpdateRangeQuery<number, number> {
return new SegmentTreeRangeUpdateRangeQuery(nOrNums, {
e: () => INF,
id: () => INF,
op: (a, b) => Math.min(a, b),
mapping: (f, x) => (f === INF ? x : f),
composition: (f, g) => (f === INF ? g : f)
})
}
/**
* 01区间翻转,查询区间和.
*/
function createRangeFlipRangeSum(
nOrNums: number | ArrayLike<[sum: number, size: number]>
): SegmentTreeRangeUpdateRangeQuery<[sum: number, size: number], number> {
return new SegmentTreeRangeUpdateRangeQuery<[sum: number, size: number], number>(nOrNums, {
e: () => [0, 1],
id: () => 0,
op: ([sum1, size1], [sum2, size2]) => [sum1 + sum2, size1 + size2],
mapping: (f, [sum, size]) => (f === 0 ? [sum, size] : [size - sum, size]),
composition: (f, g) => f ^ g
})
}
/**
* 区间赋值区间加,区间和.
*/
function createRangeAssignRangeAddRangeSum(
nOrNums: number | ArrayLike<[size: number, sum: number]>
): SegmentTreeRangeUpdateRangeQuery<[size: number, sum: number], [mul: number, add: number]> {
return new SegmentTreeRangeUpdateRangeQuery<
[size: number, sum: number],
[mul: number, add: number]
>(nOrNums, {
e() {
return [1, 0]
},
id() {
return [1, 0]
},
op(e1, e2) {
return [e1[0] + e2[0], e1[1] + e2[1]]
},
mapping(lazy, data) {
return [data[0], data[1] * lazy[0] + data[0] * lazy[1]]
},
composition(f, g) {
return [f[0] * g[0], f[0] * g[1] + f[1]]
},
equalsId(id1, id2) {
return id1[0] === id2[0] && id1[1] === id2[1]
}
})
}
/**
* 区间仿射变换,区间和.
*/
function createRangeAffineRangeSum(
nOrNums: number | ArrayLike<[size: bigint, sum: bigint]>,
bigMod: bigint
): SegmentTreeRangeUpdateRangeQuery<[size: bigint, sum: bigint], [mul: bigint, add: bigint]> {
return new SegmentTreeRangeUpdateRangeQuery(nOrNums, {
e() {
return [1n, 0n]
},
id() {
return [1n, 0n]
},
op(e1, e2) {
return [e1[0] + e2[0], (e1[1] + e2[1]) % bigMod]
},
mapping(lazy, data) {
return [data[0], (data[1] * lazy[0] + data[0] * lazy[1]) % bigMod]
},
composition(f, g) {
return [(f[0] * g[0]) % bigMod, (f[0] * g[1] + f[1]) % bigMod]
},
equalsId(id1, id2) {
return id1[0] === id2[0] && id1[1] === id2[1]
}
})
}结尾

评论 (15)
排序:最热
