前言
楼主深刻感到自己动归的水平太差
痛定思痛,决定爆刷一些dp的题
因此在力扣上搜集了一些树形dp的题练习下,以本文作为记录
注意:本文不适合连一点树形dp概念的小白观看,且不会写过多文字作题解,一些尽在代码中
🔖注意点
有些题目是表明是二叉树,但是在实际做题的时候,请以多叉树的思路进行考虑。写一些其他树的相关题目也是如此。
当然如果想快速ac确实可以上二叉树,但平时练习请自我约束。
🔖思路与技巧
树形dp,比其他的一些dp专题比起来。有一个特点就是能画图(不是说别的不能画),可以借助图像来辅助思考。
对于比较特殊的一类(换根dp)。
其实很多时候题目要求解的会很表明:
- 一般是一颗无根树
- 要求从任意点都可以作为根然后查看树的状态
注意到底是谁贡献给谁。一般来说通过递归是将子树的状态贡献给当前访问节点,但是也有部分当前节点影响子树的状态的题型。
说白了就是自顶向下与自低向上的区别。
🔖碎碎念
其他大多数oj属于输入输出模式,这种模式的所有数据结构都要自己构造,完全可以根据自己的喜好习惯之类的。
而在力扣做题是核心函数形式,有些题会给出构造好的链式树,当然也可以重新re构造自己的数据结构。这点其实对选手的能力更为考验。当然本文的核心还是在树形dp的思维上,请不要被次要点而分心。
本文有些题,并非是纯纯的树形dp的样子,但是楼主认为这写题中也包含着比价浓厚的树形思维,建图,遍历等等,因此也会纳入本文。
(优美的中国话)越做到后面的一些题,越感觉自己被骗了。说到底树形dp,核心还是考dp。还是考验状态的定义和转移的方式,树形只是一种辅助的数据逻辑关系手段。确实有一部分题是和树形强相关的,但是大多数都可以将逻辑扁平化成线性逻辑关系。
说到底还是个人思维较差,水平有限,自勉!
题单
🏷️124. 二叉树中的最大路径和
⭐树的直径变形
题意与思路
求路径最大和
即:求出链的最大和
根据当前点作为一个转折点
当变为多叉树时,写个循环操作即可
Code
class Solution {
private:
// 注意,节点有负值
int ans = INT_MIN;
// 以root为根的子树的一条链的最大值
int dfs(TreeNode* root, int sum) {
// null,当前无贡献
// 无贡献就是0,就当找个空树的贡献是0
if (root == nullptr) {
return 0;
}
// 获取左右链的最大值
int left = dfs(root->left, 0);
int right = dfs(root->right, 0);
// 维护答案
// 当前节点+左右子树的最大值
// 就是将当前root作为一个转折
ans = max(ans, root->val + left + right);
// 连接当前root,构成一条链
int res = max(left, right) + root->val;
// 本题会出现负数
return max(res, 0);
}
public:
int maxPathSum(TreeNode* root) {
dfs(root, 0);
return ans;
}
};🏷️310. 最小高度树
⭐经典换根dp + 统计深度
题意与思路
有一个树,可以以任意节点为根。
统计出深度最小的树的集合。
本题有其他证明和思路(但比较难证明),但更加通用的解法为换根dp。
这是一道非常经典的换根dp。
- dfs0 统计出以root为根时,其他所有子树的深度
- dfs1 维护每次换根时的深度,注意每次换根时
cur->nex有两个步骤- 重新维护cur相对于nex的状态
- 记录nex (为了防止特殊情况,可以放在dfs开栈的开头,递归子节点前)
Code
class Solution {
private:
vector<vector<int>> grap;
private:
// 第一轮dfs
// 获取以root为根时,各个子树的深度
void dfs0(int cur, int from, vector<int>& deep) {
deep[cur] = 1;
for (int nex : grap[cur]) {
if (from == nex) {
continue;
}
// 先搜索子树,获取子树的状态
dfs0(nex, cur, deep);
deep[cur] = max(deep[cur], deep[nex] + 1);
}
}
// 换根dp
void dfs1(int cur, int from, vector<int>& deep, vector<int>& ans) {
// 找出最大和次大值
int first = 0, second = 0;
for (int nex : grap[cur]) {
int val = deep[nex];
if (val >= first) {
second = first;
first = val;
} else if (val > second) {
second = val;
}
}
// 1. 记录当前ans
// 记录cur的最大值
ans[cur] = first + 1;
for (int nex : grap[cur]) {
if (nex == from) {
continue;
}
// 2. 维护下一个栈时吗,当前cur相对下一个栈的状态
// 更新cur的深度
// 这里指的是,换到nex后
// 目前这个栈的cur的深度,要相对nex栈做主变化
if (deep[nex] != first) {
deep[cur] = first + 1;
} else {
deep[cur] = second + 1;
}
dfs1(nex, cur, deep, ans);
}
}
public:
vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
grap = vector<vector<int>>(n);
for (auto&& e : edges) {
int u = e[0], v = e[1];
grap[u].push_back(v);
grap[v].push_back(u);
}
vector<int> dp(n);
dfs0(0, -1, dp);
vector<int> eachDeep(n);
dfs1(0, -1, dp, eachDeep);
// 回归到本题,找出深度最小的序列
int minn = *min_element(eachDeep.begin(), eachDeep.end());
vector<int> ans;
for (int i = 0; i < n; i += 1) {
if (minn == eachDeep[i]) {
ans.push_back(i);
}
}
return ans;
}
};🏷️337. 打家劫舍 III
⭐选与不选,经典dp
题意与思路
在树形结构中,不能选临近的点,计算能获得权值的最大值。
先掌握最基本的:198. 打家劫舍 理解动归的取与不取的思想。
维护两个状态:
- 选取当前
- 不选当前
转移:
- 选当前,则子节点不能选
- 不选当前,则子节点状态任意
类似的题:
洛谷:P1352 没有上司的舞会
Code
class Solution {
private:
pair<int, int> dfs(TreeNode* root) {
// 选择当前点
int need = root->val;
// 不选当前点
int needless = 0;
for (auto nex : {root->left, root->right}) {
if (nex == nullptr) {
continue;
}
// 获取子树状态
auto [sonNeed, sonNeedless] = dfs(nex);
// 选了当前,则子节点不能选
need += sonNeedless;
// 不选当前,则子节点状态任意
needless += max(sonNeed, sonNeedless);
}
return {need, needless};
}
public:
int rob(TreeNode* root) {
auto [need, needless] = dfs(root);
return max(need, needless);
}
};🏷️543. 二叉树的直径
⭐⭐经典树形dp
题意与思路
找一条最长的链
其实就是通过dfs记录深度,并维护当前遍历点左右的最深深度。
Code
class Solution {
private:
int ans = 0;
// 以root为根的子树,能贡献的最长链条
// 反参就是root的链的最长
int dfs(TreeNode* root) {
// 空节点,贡献0
if (root == nullptr) {
return 0;
}
int left = dfs(root->left);
int right = dfs(root->right);
// 以root为转折点,构成的链的长度(也就是本题的树的直径)
ans = max(ans, left + right);
// 左右中最长的 + 当前的root自己
return max(left, right) + 1;
}
public:
int diameterOfBinaryTree(TreeNode* root) {
dfs(root);
return ans;
}
};🏷️687. 最长同值路径
⭐两个节点之间的路径长度
题意与思路
两个节点之间的路径长度
543. 二叉树的直径 的加强版,在原有的基础上规定了路径上的每个节点具有相同值
Code
class Solution {
private:
int ans = 0;
// 以root为根的子树的最长链
int dfs(TreeNode* root) {
if (root == nullptr) {
return 0;
}
vector<int> res = {0, 0};
int left = dfs(root->left);
int right = dfs(root->right);
if (root->left && root->left->val == root->val) {
res.push_back(left);
}
if (root->right && root->right->val == root->val) {
res.push_back(right);
}
sort(res.begin(), res.end(), greater<int>());
// 累计弯折的两边,注意本题记录的是边数
ans = max(ans, res[0] + res[1]);
// 返回最长的链(的点数)
return res[0] + 1;
}
public:
int longestUnivaluePath(TreeNode* root) {
dfs(root);
return ans;
}
};🏷️799. 香槟塔
⭐自顶向下的树形
题意与思路
如下所示的,由顶部杯子向下层杯子提供贡献。
求目标杯子中会有多少体积。
这是一道自顶向下的题目。
就如图一般,可以抽象成一棵树。不断的向下贡献,具体的可以用二维数组进行表示。
最后注意,一个杯子最小容纳0,最大容纳1
Code
class Solution {
public:
double champagneTower(int poured, int query_row, int query_glass) {
// 树形dp,由上层的两个节点各贡献一半
vector<vector<double>> dp(query_row + 1, vector<double>(query_glass + 1));
// 树根打满
dp[0][0] = poured;
for (int row = 1; row <= query_row; row += 1) {
for (int col = 0; col <= query_glass; col += 1) {
// 假设同列和前一列的贡献
double sum = 0.0;
// 从右上角的杯子获取贡献
sum += max(dp[row - 1][col] - 1, 0.0) / 2;
if (col > 0) {
// 从左上角的杯子获取贡献
sum += max(dp[row - 1][col - 1] - 1, 0.0) / 2;
}
dp[row][col] = max(0.0, sum);
}
}
return min(1.0, dp[query_row][query_glass]);
}
};🏷️823. 带因子的二叉树
⭐构造+子树的贡献
题意与思路
有一组不重复的数字。每个数可以用任意次。
每个非叶节点是左右子节点的乘积。
正整数乘积,必然是小值贡献到大值,因此排序。
一个节点又子树构成,左右子树一起贡献出来,也是一个乘积(乘法贡献)
Code
class Solution {
private:
constexpr static int mod = 1e9 + 7;
public:
int numFactoredBinaryTrees(vector<int>& arr) {
int n = arr.size();
// 有序递增
sort(arr.begin(), arr.end());
// 维护以key为根节点的时候,可行的种类
unordered_map<int, int64_t> cnt;
int64_t ans = 0;
for (int i = 0; i < n; i += 1) {
// 单个点也是一棵树
cnt[arr[i]] = 1;
// 枚举比当前arr[i]小的点
for (int j = 0; j < i; j += 1) {
if (arr[i] % arr[j] != 0) {
continue;
}
int x = arr[i] / arr[j];
// 累计子节点能给出的贡献
// [10, 2, 5], [10, 5, 2]是两种,但是随着遍历都能计算到
// 当前10
// 假设存在2,5分别遍历到的时候会给出贡献
// 假设存在2,没有5那么cnt[5]的贡献就是0
cnt[arr[i]] += cnt[arr[j]] * cnt[x];
cnt[arr[i]] %= mod;
}
ans += cnt[arr[i]];
ans %= mod;
}
return ans;
}
};🏷️834. 树中距离之和
⭐⭐经典换根dp
题意与思路
求任意点作为root,与所有其他节点之间的距离之和
经典换根dp
注意求dfs0的默认和需要思考怎么利用深度这点。当然还有一种写法,由于只需要一个dfs0的root值。
可以直接传递一个变量的引用,然后唯一一个deep值,再不断再递归栈中累计即可。
dfs1也是非常经典的,根据点数进行维护。
其中,注意每次递归时的cur。其实就是root。总点数n,总边数n-1。
类似的题:洛谷 P3478
Code
class Solution {
private:
vector<vector<int>> grap;
int n;
private:
// 距离和 => 深度和
void dfs0(int cur, int from, vector<int>& size, vector<int> &deepSum) {
// 节点数初始1
// 深度初始0,边数
size[cur] = 1;
deepSum[cur] = 0;
for (int nex : grap[cur]) {
if (nex == from) {
continue;
}
// 先递归子树,获取子树状态
dfs0(nex, cur, size, deepSum);
// 累计子树元素个数
size[cur] += size[nex];
// 统计到子树各个点的距离
// 子树的距离和 + 子树中每个点到cur的一个单位的距离
deepSum[cur] += deepSum[nex] + size[nex];
}
}
// 换根
void dfs1(int cur, int from, vector<int>& size, vector<int>& ans, int sum) {
// 入dfs时,记录答案
ans[cur] = sum;
for (int nex : grap[cur]) {
if (nex == from) {
continue;
}
// 对于在当前dfs的cur,其实就是root
// 而root的总和是固定的n-1,点数是n
// 换根后的调整
int nexSum = sum;
// nex子树的点,贡献-1
nexSum += -size[nex];
// nex子树以外的点,贡献+1
nexSum += n - size[nex];
dfs1(nex, cur, size, ans, nexSum);
}
}
public:
vector<int> sumOfDistancesInTree(int n, vector<vector<int>>& edges) {
this->n = n;
grap = vector<vector<int>>(n);
for (auto&& e : edges) {
int u = e[0], v = e[1];
grap[u].push_back(v);
grap[v].push_back(u);
}
// 在[0, n-1]任意一点均可
const int root = 0;
// 主要是算出,以root的题目要求和
vector<int> deepSum(n);
// 子树节点数量
vector<int> size(n);
dfs0(root, -1, size, deepSum);
// 换根
vector<int> ans(n);
dfs1(root, -1, size, ans, deepSum[root]);
return ans;
}
};🏷️968. 监控二叉树
⭐分类讨论状态转移
题意与思路
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
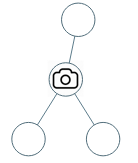
本题读完会有一种图的感觉,因为父子节点都可以辐射到当前节点。但是如果当成图来做的话会非常苦难。
这里直接将树形dp的思路:
要让整棵树成为稳态,一个节点只有三种状态可能。
- 当前节点放摄像
- 父节点放摄像
- 子节点放摄像
因此每个节点维护三个状态,并考虑三个状态是如何靠递归的子树进行转移的。
- 当前节点self
- 则两个子节点可以是任意状态
- min(left) + min(right) + val(val是当前节点的贡献,放在本题就是1)
- 靠父节点放摄像
- 当前靠父节点,那么当前不能辐射到子节点
- 子节点只能靠自己或者孙子节点
- min(left子, left孙) + min(right子, right孙)
- 靠子节点放摄像
- 只要保证孩子节点中至少有一个放摄像即可,二叉树有2x2-1=3种可能
- min(left + right, left + right孙, left孙 + right)
递归截至条件,空节点:
不能放摄像,也不需要被辐射
进阶与化简可以参考灵神的讲解:灵神题解 968. 监控二叉树
Code
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
// 当前节点放摄像
// 父节点放摄像
// 子节点放摄像
tuple<int, int, int> dfs(TreeNode* root) {
// 空节点不能放摄像
// 也没有父子节点的监控信息
if (nullptr == root) {
return {INT_MAX / 2, 0, 0};
}
auto [lSelf, lFa, lSon] = dfs(root->left);
auto [rSelf, rFa, rSon] = dfs(root->right);
// 自己放了,左右孩子可以任意状态
int self = min({lSelf, lFa, lSon}) + min({rSelf, rFa, rSon}) + 1;
// 靠当前父节点,则孩子不能靠当前
int fa = min(lSelf, lSon) + min(rSelf, rSon);
// 靠孩子节点,则至少有一个孩子设摄像机。且这些孩子不能靠当前
int son = min({lSelf + rSelf, lSelf + rSon, lSon + rSelf});
return {self, fa, son};
}
public:
int minCameraCover(TreeNode* root) {
auto [self, fa, son] = dfs(root);
return min(self, son);
}
};🏷️1289. 下降路径最小和 II
⭐⭐经典数塔
题意与思路
给你一个 n x n 整数矩阵 grid ,请你返回 非零偏移下降路径 数字和的最小值。
非零偏移下降路径 定义为:从 grid 数组中的每一行选择一个数字,且按顺序选出来的数字中,相邻数字不在原数组的同一列。
超级经典数塔,经典树形自底向上贡献。
洛谷:P1216

Code
class Solution {
public:
int minFallingPathSum(vector<vector<int>>& grid) {
const int n = grid.size();
int index[n];
for (int i = 1; i < n; i += 1) {
auto&& preLevel = grid[i - 1];
// 按照下标排序,目前是找出最小和次小的
iota(index, index + n, 0);
sort(index, index + n, [&](int x, int y) {
return preLevel[x] < preLevel[y];
});
// 从最小和次小的中选取
// 垂直上方的不能选
for (int j = 0; j < n; j += 1) {
if (j == index[0]) {
grid[i][j] += preLevel[index[1]];
} else {
grid[i][j] += preLevel[index[0]];
}
}
}
return *min_element(grid.back().begin(), grid.back().end());
}
};🏷️1372. 二叉树中的最长交错路径
⭐最长交叉路径
题意与思路
如图所示,找出一左一右的最长路径
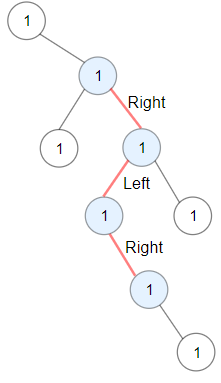
维护所有方向的深度即可
Code
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
private:
int ans = 0;
// 左拐的最大值
// 右拐的最大值
tuple<int, int> dfs(TreeNode* root) {
if (nullptr == root) {
return {0, 0};
}
auto [lLMax, lRMax] = dfs(root->left);
auto [rLMax, rRMax] = dfs(root->right);
ans = max(ans, rLMax);
ans = max(ans, lRMax);
return {lRMax + 1, rLMax + 1};
}
public:
int longestZigZag(TreeNode* root) {
dfs(root);
return ans;
}
};🏷️1373. 二叉搜索子树的最大键值和
⭐判断搜索树 模板
题意与思路
给你一棵以 root 为根的 二叉树 ,请你返回 任意 二叉搜索子树的最大键值和。
二叉搜索树的定义如下:
- 任意节点的左子树中的键值都 小于 此节点的键值。
- 任意节点的右子树中的键值都 大于 此节点的键值。
- 任意节点的左子树和右子树都是二叉搜索树。
注意搜索树的性质: 左 < 根 < 右
同时维护子树的权值和。
同类型题:
Code
class Solution {
private:
int ans = 0;
private:
// 子树中所有节点的最小值
// 子树中所有节点的最大值
// 是否是搜索树
// 子树权值和
tuple<int, int, bool, int> dfs(TreeNode* root) {
const int curVal = root->val;
// 叶节点
if (root->left == nullptr && root->right == nullptr) {
ans = max(ans, curVal);
return {curVal, curVal, true, curVal};
}
bool flag = true;
int minn = curVal, maxx = curVal;
int nodeSum = curVal;
// 通过子树的最大最小值来判断是否是搜索树
auto searchSon = [&](TreeNode* son, auto&& op) {
if (nullptr == son) {
return ;
}
auto [sMin, sMax, sFlag, sSum] = dfs(son);
flag &= op(curVal, sMin);
flag &= op(curVal, sMax);
flag &= sFlag;
minn = min(minn, sMin);
maxx = max(maxx, sMax);
nodeSum += sSum;
};
// 搜索树的性质
// 根 > 左
searchSon(root->left, greater<>());
// 根 < 右
searchSon(root->right, less<>());
// 是搜索树则进行ans的松弛
if (flag) {
ans = max(ans, nodeSum);
}
return {minn, maxx, flag, nodeSum};
}
public:
int maxSumBST(TreeNode* root) {
// 非空树
dfs(root);
return ans;
}
};🏷️1377. T 秒后青蛙的位置
⭐自顶向下的概率贡献
题意与思路
***从根节点往下跳,不能返回。求给定一个节点,问这个节点是最后落脚点的概率。
很明显的自顶向下搜素,维护一下概率传递到下一层。
本题用bfs更简单。
Code
class Solution {
public:
double frogPosition(int n, vector<vector<int>>& edges, int t, int target) {
// [1, n]
// 无向树,但不是图
vector<vector<int>> grap(n + 1);
for (auto&& e : edges) {
grap[e[0]].push_back(e[1]);
grap[e[1]].push_back(e[0]);
}
grap[1].push_back(-1);
// 父节点 位置 概率
using qNode = tuple<int, int, double>;
queue<qNode> q;
// 起点规定为1
q.push({-1, 1, 1.0});
// 自顶向下的bfs
vector<qNode> endNode;
while (t--) {
int len = q.size();
while (len--) {
auto [from, cur, d] = q.front();
q.pop();
if (grap[cur].size() == 1) {
endNode.push_back({from, cur, d});
continue;
}
// 树形结构,因此不用记录vis
for (auto nex : grap[cur]) {
if (from == nex) {
continue;
}
q.push({cur, nex, d / (grap[cur].size() - 1)});
}
}
}
while (q.size()) {
endNode.push_back(q.front());
q.pop();
}
for (auto&& [from, cur, d] : endNode) {
if (target == cur) {
return d;
}
}
return 0;
}
};🏷️1519. 子树中标签相同的节点数
⭐子树状态贡献给父节点
题意与思路
统计当前子树下有多少个权值相等的点。
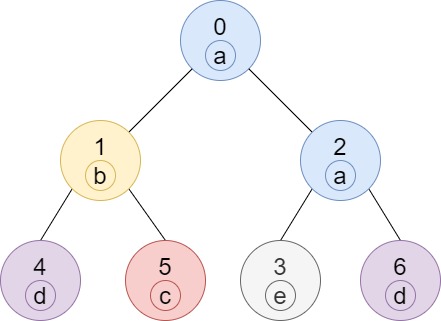
一般遇到这种统计字符的不要怕,直接梭哈统计所有字符,这个复杂度是常量级的。即使是128个字符,也是常量级的(虽说常量系数却是大了点)。
典型了子树状态贡献给子树根。
Code
class Solution {
private:
vector<vector<int>> grap;
string s;
vector<int> ans;
private:
using Arr26 = array<int, 26>;
// 整体状态返回
Arr26 dfs(int cur, int from) {
Arr26 cnt{};
cnt[s[cur] - 'a'] += 1;
for (int nex : grap[cur]) {
if (nex == from) {
continue;
}
// 子树状态贡献给当前
auto&& nexCnt = dfs(nex, cur);
for (int i = 0; i < cnt.size(); i += 1) {
cnt[i] += nexCnt[i];
}
}
// 维护答案
ans[cur] = cnt[s[cur] - 'a'];
return cnt;
}
public:
vector<int> countSubTrees(int n, vector<vector<int>>& edges, string labels) {
grap.resize(n);
s = labels;
ans.resize(n);
for (auto&& e : edges) {
grap[e[0]].push_back(e[1]);
grap[e[1]].push_back(e[0]);
}
// 题目规定root=0
dfs(0, -1);
return ans;
}
};🏷️1617. 统计子树中城市之间最大距离
⭐状压枚举 + 树的直径
题意与思路
题意,有一颗无向树。统计树种所有子树的直径。
观察到数据量较小,直接状压枚举所有子树的可能性。并对这个子集进行树的直径的搜索。
注意搜索是针对这个子集的。
本题难度较大,且有多种解法,请直接查看:
Code
class Solution {
private:
vector<vector<int>> grap;
private:
// 注意,题目求的是边的个数
int dfs(int cur, int& mask, int& length) {
// 从mask集合中删除该店
mask &= ~(1 << cur);
// 记录子树直径
vector<int> arr;
for (int nex : grap[cur]) {
// 在mask这个子集中,才能贡献出直径
if ((mask & (1 << nex)) == 0) {
continue;
}
// 两点贡献出一条边
int val = dfs(nex, mask, length) + 1;
arr.push_back(val);
}
// 树的直径
arr.push_back(0);
arr.push_back(0);
sort(arr.begin(), arr.end(), greater{});
length = max(length, arr[0] + arr[1]);
return arr[0];
}
public:
vector<int> countSubgraphsForEachDiameter(int n, vector<vector<int>>& edges) {
grap.resize(n);
for (auto&& e : edges) {
// [1, n] -> [0, n)
int u = e[0] - 1, v = e[1] - 1;
grap[u].push_back(v);
grap[v].push_back(u);
}
vector<int> ans(n - 1);
const int MASK = 1 << n;
for (int mask = 1; mask < MASK; mask += 1) {
// 在mask这个子集中找打一个点作为root
// __builtin_ctz 计算右起0的个数
int root = __builtin_ctz(mask);
int vis = mask;
int length = 0;
dfs(root, vis, length);
// 如果vis都经历到了,且是有效直径
// 则可以记录答案
if (vis == 0 && length > 0) {
// 题意要求存储len=1开始
ans[length - 1] += 1;
}
}
return ans;
}
};🏷️2246. 相邻字符不同的最长路径
⭐有限制的最长路径
题意与思路
树中每个点都有一个字符,寻找没有连续字符的最长路径
在最长路径的基础上加入限制。
注意本题是普通树,而以转角构成链只可以借两个子树。编码时注意处理细节。
Code
class Solution {
private:
vector<vector<int>> grap;
string s;
int n;
private:
int ans = 0;
// 以root为根的最长合法链
int dfs(int root) {
const char ch = s[root];
vector<int> son;
for (int nex : grap[root]) {
// 合法
if (ch != s[nex]) {
int val = dfs(nex);
son.push_back(val);
}
// 相同,不给出贡献
// 但从搜索的完整性上,还是要搜
else {
dfs(nex);
}
}
// 注意,本题不是二叉树
// 这里模拟为当前root向下的两条链
// 为了保证编码的便利,增加两个0点
son.push_back(0);
son.push_back(0);
sort(son.begin(), son.end(), greater<int>());
ans = max(ans, son[0] + son[1] + 1);
return son[0] + 1;
}
public:
int longestPath(vector<int>& parent, string s) {
this->n = s.size();
this->s = s;
grap = vector<vector<int>>(n);
for (int i = 1; i < n; i += 1) {
grap[parent[i]].push_back(i);
}
// 本题规定0为root
int root = 0;
dfs(root);
return ans;
}
};🏷️2477. 到达首都的最少油耗
⭐有限制的深度问题+子树贡献
题意与思路
题目等价于给出了一棵以节点 0 为根结点的树,并且初始树上的每一个节点上都有一个人,现在所有人都需要通过「车子」向结点 0 移动。
题目的描述一定程度上比较谜
有限制的深度问题。规定一次统一带走的最大数目。
还是分解子问题,查看子树能贡献来多少人,若坐满车了,则直接一波带走。
官方是用的循环迭代累计的方式,我这里直接获得最终贡献,本质是类似的。
Code
class Solution {
private:
vector<vector<int>> grap;
vector<int> vis;
int k;
long long ans = 0;
private:
// 当前,来向,深度
void dfs(int cur, int from, int level) {
for (int nex : grap[cur]) {
if (nex == from) {
continue;
}
dfs(nex, cur, level + 1);
// 子树有人数可以贡献上来
if (vis[nex] != 0) {
vis[cur] += vis[nex];
// 子树向上走一步
ans += 1;
if (vis[cur] > k) {
vis[cur] -= k;
// 全接走
ans += level;
}
}
} // for
}
public:
long long minimumFuelCost(vector<vector<int>>& roads, int seats) {
const int n = roads.size() + 1;
this->k = seats;
grap.resize(n);
// 每个节点至少有自己一个人
vis.resize(n, 1);
for (auto&& e : roads) {
grap[e[0]].push_back(e[1]);
grap[e[1]].push_back(e[0]);
}
dfs(0, -1, 0);
return ans;
}
};🏷️2538. 最大价值和与最小价值和的差值
⭐选与不选,经典dp思维
题意与思路
根据题意,数值最小就是根root,而链的根其实也是叶节点。
得出本质是找出一个最大和的链,而这个链的一段缺少一个叶节点。
本题还有换根dp的思路,比较难换 (留坑)
Code
class Solution {
private:
vector<vector<int>> grap;
vector<int> value;
int ans = 0;
// 返回{不带叶节点, 带叶节点}构成的链的最大值
pair<int, int> dfs(int cur, int from) {
// 不带叶节点
int sum0 = 0;
// 带叶节点
int sum1 = value[cur];
for (int nex : grap[cur]) {
if (from == nex) {
continue;
}
auto [son0, son1] = dfs(nex, cur);
// 当前不带叶 + 子树带叶
ans = max(ans, sum0 + son1);
// 当前带叶 + 子树不带叶
ans = max(ans, sum1 + son0);
// 能遍历到这里,说明cur必然不是叶节点
// 把带不带叶节点的任务交给son
sum0 = max(sum0, son0 + value[cur]);
sum1 = max(sum1, son1 + value[cur]);
}
return {sum0, sum1};
}
public:
long long maxOutput(int n, vector<vector<int>>& edges, vector<int>& price) {
grap = vector<vector<int>>(n);
value = price;
for (auto&& e : edges) {
grap[e[0]].push_back(e[1]);
grap[e[1]].push_back(e[0]);
}
// 树形dp
dfs(0, -1);
return ans;
}
};🏷️2581. 统计可能的树根数目
⭐换根dp 相邻点的边关系
题意与思路
现在有一棵无根树。
有一个猜测集合,是猜测相邻点的父子关系。
统计满足猜测正确个数 >= k的可行根的数量。
父子关系只涉及到目标的两个点,因此不用考虑从子树或者其他状态
一般来说这种涉及两个相邻点的换根转换关系如下:
- 减去原先的贡献
- 增加换根后的贡献
类似的题:
都是相邻两个点的(cur, nex)的边的影响。
Code
template<typename Type>
class HashPair {
private:
unordered_set<Type> hash;
Type getKey(Type lhs, Type rhs) {
constexpr unsigned OFFSET = (8 * sizeof(Type)) >> 1;
return (lhs << OFFSET) | rhs;
}
public:
void insert(Type lhs, Type rhs) {
hash.insert(getKey(lhs, rhs));
}
bool find(Type lhs, Type rhs) {
return hash.find(getKey(lhs, rhs)) != hash.end();
}
};
/////////////////////////////////////////////////////////////
class Solution {
private:
vector<vector<int>> grap;
private:
// 题意,满足k个
int k;
// 合法键值对
HashPair<long long> hash;
private:
// 以root维护sum
void dfs0(int cur, int from, int& sum) {
for (int nex : grap[cur]) {
if (nex == from) {
continue;
}
dfs0(nex, cur, sum);
// 统计父子节点合法数量
sum += hash.find(cur, nex);
}
}
// 通过换根维护ans
void dfs1(int cur, int from, int curSum, int& ans) {
ans += (curSum >= k);
for (int nex : grap[cur]) {
if (nex == from) {
continue;
}
// 换根后,当前的父子关系会反向
int nexSum = curSum;
// 减去当前的状态
nexSum -= hash.find(cur, nex);
// 累计反转后的新状态
nexSum += hash.find(nex, cur);
dfs1(nex, cur, nexSum, ans);
}
}
public:
int rootCount(vector<vector<int>>& edges, vector<vector<int>>& guesses, int k) {
// 树点 = 树边+1
const int n = edges.size() + 1;
this->k = k;
// 本题中合法的键值对
for (auto&& e : guesses) {
int from = e[0], to = e[1];
hash.insert(from, to);
}
// 换根dp模板流程
grap = vector<vector<int>>(n);
for (auto&& e : edges) {
int u = e[0], v = e[1];
grap[u].push_back(v);
grap[v].push_back(u);
}
const int root = 0;
int sum = 0;
dfs0(root, -1, sum);
int ans = 0;
dfs1(root, -1, sum, ans);
return ans;
}
};😭2603. 收集树中金币
😭换根dp中的战斗机 / 没有写,留个坑
存在别的解法,且非常巧妙
但是用换根dp的话会非常困难
🏷️2646. 最小化旅行的价格总和
⭐打家劫舍 III变形 (树上差分优化,LCA(Tarjan))
题意与思路
一颗树上每个点都有权值,有trips个[start, end]查询,需要记录路径上的点权
现有一次机会的操作,可以将树上不联系的点的点权减半
求能后获得总权值的最小值
给出的这操作非常的337. 打家劫舍 III 。那么问题是怎么多次访问。
方法就是暴力记录每条路,统计每个点经过的次数,贡献到点权上。遍历方法类似于2467. 树上最大得分和路径 只是2467记录的是时间戳,而这里是次数。
优化拓展
仅做简单解释:
在原先的预处理节点访问次数是暴力求解。
尝试在树上进行差分操作,以优化到常量次数处理cnt。
树上差分需要用到求LCA最近公共祖先,这里使用Tarjan算法,具体见代码或者上面的博客。
Code
class Solution {
private:
vector<vector<int>> grap;
vector<int> cnt;
vector<int> val;
private:
// 类似2467. 树上最大得分和路径
// 记录每个点的访问次数
bool dfs1(int cur, int from, int end) {
if (cur == end) {
cnt[end] += 1;
return true;
}
bool flag = false;
for (int nex : grap[cur]) {
if (nex == from) {
continue;
}
// 无向树只有一条路可以通向end
// 因此可以直接截断
flag |= dfs1(nex, cur, end);
if (flag) {
break;
}
}
// 如果是路径上的点,则+1
cnt[cur] += flag;
return flag;
}
// 打家劫舍 III
// 不减半的
// 减半的值
pair<int, int> dfs2(int cur, int from) {
int all = val[cur];
int half = all / 2;
for (int nex : grap[cur]) {
if (nex == from) {
continue;
}
auto [sAll, sHalf] = dfs2(nex, cur);
all += min(sAll, sHalf);
half += sAll;
}
return {all, half};
}
public:
int minimumTotalPrice(int n, vector<vector<int>>& edges, vector<int>& price, vector<vector<int>>& trips) {
val.resize(n);
cnt.resize(n);
grap.resize(n);
// 建图
for (auto&& e : edges) {
grap[e[0]].push_back(e[1]);
grap[e[1]].push_back(e[0]);
}
// 第一轮dfs统计所有点的访问次数
for (auto&& arr : trips) {
int start = arr[0], end = arr[1];
dfs1(start, -1, end);
}
// 访问次数贡献到权值上
// 没经过的点就是cnt=0不会在最后有贡献
for (int i = 0; i < n; i += 1) {
val[i] = price[i] * cnt[i];
}
// 遍历整颗树,没过的点贡献为0不影响答案
auto [all, half] = dfs2(0, -1);
return min(all, half);
}
};🏷️2858. 可以到达每一个节点的最少边反转次数
⭐换根dp root&son作为一个整体获取贡献
题意与思路
在一个有向的树形结构中。
计算所有点,到达其他所有点的,需要反转的边的数量。
root&son作为一个整体获取贡献。
将这两个点作为一个整体,其他所有点的边对这两个点的贡献是一样的。受影响的只是这两个点的连接边决定。
就是说abs(dp[root] - dp[son]) == 1相邻的两个点的差值必然为1。
class Solution {
private:
using pii = pair<int, int>;
vector<vector<pii>> grap;
const int root = 0;
private:
// 计算初始root的dp
void dfs0(int cur, int from, vector<int>& dp) {
for (auto&& [nex, val] : grap[cur]) {
if (nex == from) {
continue;
}
// 搜索所有子树
dfs0(nex, cur, dp);
// 所有的遍历结果贡献到root上
if (val < 0) {
dp[root] += 1;
}
}
}
// 换根dp
void dfs1(int cur, int from, vector<int>& dp) {
for (auto&& [nex, val] : grap[cur]) {
if (nex == from) {
continue;
}
// 仅反转临近边的方向即可,其余的方向贡献是不变的
// 可以理解为把这两个点合并到一起作为一个node
// 其他点的边的方向对这个node的贡献是一样的
// 到临近边是正向
if (val > 0) {
dp[nex] = dp[cur] + 1;
}
// 到临近边是负向
else {
dp[nex] = dp[cur] - 1;
}
// 先换根维护好,再递归换根后的状态
dfs1(nex, cur, dp);
}
}
public:
vector<int> minEdgeReversals(int n, vector<vector<int>>& edges) {
grap = vector<vector<pii>>(n);
for (auto&& e : edges) {
const int from = e[0], to = e[1];
// 正向边
grap[from].push_back({to, 1});
// 逆向边
grap[to].push_back({from, -1});
}
vector<int> dp(n);
dfs0(root, -1, dp);
dfs1(root, -1, dp);
return dp;
}
};🏷️2867. 统计树中的合法路径数目
⭐⭐状态机转移
题意与思路
有一个无根树,每个节点序号序号唯一。
求两个节点间只有一个质数的路径的个数。(1 -> 5) 和 (5 -> 1)视为一条路径。
法一:传统树形dp
本题最大的一个限制是只有一个质数。思考两个问题:
- 如何产生这么一个序列
- 生成序列后是否会一直合法
可见是这么一个过程:
- 没有质数的序列
- 有一个质数的序列
- 超过一个质数的序列
显然第三点是可以直接略去的,因此我们只维护两个状态。
法二:以质数为根搜索合数的联通分量大小
一个比较普遍的合法序列模型是合数 - 质数 - 合数。
因此我们直接枚举所有的质数,再搜索每个分支的联通分量的节点个数。
处理联通分量的方法比较多,单次搜索可以直接使用dfs,多次可以使用并查集。
并查集的话就是合并的模板,而dfs的化可以使用类似记忆化的方式来处理每个联通块。
Code
class PrimeSieve {
private:
int n;
// false 质数
// true 合数
vector<bool> isPrime;
vector<int> primeList;
public:
PrimeSieve(int n = 1e4 + 10) : isPrime(n + 1), n(n) {
isPrime[0] = isPrime[1] = true;
sieve();
}
bool operator[](size_t idx) const {
return !isPrime[idx];
}
private:
// 欧拉筛
void sieve() {
for (int i = 2; i <= n; i++) {
if (!isPrime[i]) {
primeList.push_back(i);
}
for (int j = 0; j < primeList.size(); j++) {
if (i * primeList[j] > n) {
break;
}
isPrime[i * primeList[j]] = true;
if (i % primeList[j] == 0) {
break;
}
}
} // for
}
};
const PrimeSieve prime(1e5 + 10);
class Solution {
private:
using ll = long long;
vector<vector<int>> grap;
ll ans = 0;
/**
* `一个`质数的序列
* `没有`质数的序列(全是合数)
*/
tuple<ll, ll> dfs(int cur, int from) {
ll onePrime = 0; // 有一个质数
ll zeroPrime = 0; // 都是合数
if (prime[cur]) {
onePrime = 1;
} else {
zeroPrime = 1;
}
for (int nex : grap[cur]) {
if (nex == from) {
continue;
}
auto [sone, szero] = dfs(nex, cur);
// 乘法原理,当前子树叠加前驱的状态
ans += onePrime * szero + zeroPrime * sone;
/**
* 根据当前是否是质数来叠加
* 不是nex,将子节点的贡献一致
* * 质数
* cur质数 += nex合数
* * 合数
* cur质数 += nex质数
* cur合数 += nex合数
*/
if (prime[cur]) {
onePrime += szero;
} else {
onePrime += sone;
zeroPrime += szero;
}
}
return {onePrime, zeroPrime};
}
public:
long long countPaths(int n, vector<vector<int>>& edges) {
grap.resize(n + 1);
for (auto&& e : edges) {
int u = e[0], v = e[1];
grap[u].push_back(v);
grap[v].push_back(u);
}
// 无向树
// 任意一个节点,拎出来为都可以为根
dfs(1, -1);
return ans;
}
};🏷️2920. 收集所有金币可获得的最大积分
⭐自顶向下的影响传递&指数级状态变化&记忆化搜索
题意与思路
一棵有权树。从根开始取值,每次取值两种操作
- coins[i] - k
- floor(coins[i] / 2) 且子树中每个点权也要折半
求最大总和
这是很典型的一种由根影响子树状态的题。
与常规的直接从子树状态贡献给当前不一样。
需要从当前把变化状态传递给子树,因此状态会指数级递增。
优化方式
- 记忆化
- 减枝
观察本题数据量,折半次数最大std::ceil(std::log2(10000))。这就优化突破点。
Code
class Solution {
private:
// 根据本题的数据量,算出最大的位移大小
static inline int Max = std::ceil(std::log2(10000));
private:
vector<vector<int>> grap;
vector<vector<int>> vis;
vector<int> value;
int k;
// 当前点,前驱点,➗2次数
int dfs(int cur, int from, int cnt) {
int& ans = vis[cur][cnt];
if (ans != -1) {
return ans;
}
int val = value[cur] >> cnt;
// 折半次数有限
int nexCnt = min(cnt + 1, Max);
int all = val - k;
int half = val >> 1;
for (int nex : grap[cur]) {
if (nex == from) {
continue;
}
all += dfs(nex, cur, cnt);
half += dfs(nex, cur, nexCnt);
}
return ans = max(all, half);
}
public:
int maximumPoints(vector<vector<int>>& edges, vector<int>& coins, int k) {
const int n = coins.size();
this->k = k;
this->value = coins;
this->grap.resize(n);
// 记忆化,-1表示未访问
// 虽然操作1需要val-k,但是操作二只是折半,因此最低值不可能为负数
this->vis = vector<vector<int>>(n, vector<int>(Max + 1, -1));
for (auto&& e : edges) {
grap[e[0]].push_back(e[1]);
grap[e[1]].push_back(e[0]);
}
// 当前点,前驱点,➗2次数
return dfs(0, -1, 0);
}
};🏷️2925. 在树上执行操作以后得到的最大分数
⭐正逆向思维
题意与思路
在有权,有根树中。
保证从根节点到叶节点的每条路径上,至少有一个点权还存在(健康树)。其余权值贡献出来。
求最大贡献值。
这个题面有点绕。
很明显的一个思维,选与不选。但直接考虑每个点便利到时选或不选有点困难。
从直接提问的角度思考,健康树与不健康树
- 不健康树 的最大值就是子树和
- 健康树
- 子树都健康,当前点贡献出去
- 将当前点作为健康点,子树和-当前点
其实本题还可以从逆向思维考虑。
- 总权值-保留点
Code
class Solution {
using ll = long long;
private:
vector<vector<int>> grap;
vector<int> value;
private:
// 正向思维
// 不健康 最大值即为子树和
// 健康
tuple<ll, ll> dfs(int cur, int from) {
// 叶子节点
if (grap[cur].size() == 1) {
return {value[cur], 0};
}
ll notHealth = value[cur];
ll health = 0;
for (int nex : grap[cur]) {
if (nex == from) {
continue;
}
auto [sNotHeath, sHeath] = dfs(nex, cur);
notHealth += sNotHeath;
health += sHeath;
}
return {notHealth, max(
health + value[cur], // 子树都健康,则当前点可以贡献出去
notHealth - value[cur] // 当前点作为健康点
)};
}
public:
long long maximumScoreAfterOperations(vector<vector<int>>& edges, vector<int>& values) {
const int n = values.size();
this->value = values;
grap.resize(n);
for (auto&& e : edges) {
grap[e[0]].push_back(e[1]);
grap[e[1]].push_back(e[0]);
}
// 辅助判叶结点
grap[0].push_back(-1);
auto [notHealth, health] = dfs(0, -1);
return health;
}
};🏷️LCP 34. 二叉树染色
⭐打家劫舍3进阶版
题意与思路
小扣有一个根结点为 root 的二叉树模型,初始所有结点均为白色,可以用蓝色染料给模型结点染色,模型的每个结点有一个 val 价值。小扣出于美观考虑,希望最后二叉树上每个蓝色相连部分的结点个数不能超过 k 个,求所有染成蓝色的结点价值总和最大是多少?
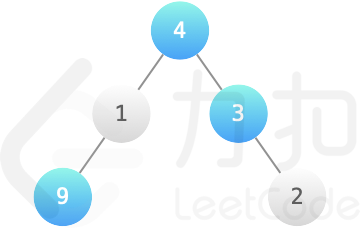
337. 打家劫舍 III 进阶版,由原来的一个接一个间隔。
变为了连续k个,直接维护k个状态,每个都需要转移松弛。
Code
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
private:
int k;
private:
// dp[k + 1]
// dp[0] 表示当前不染色
// dp[i] 表示以当前点为根的子树连续染色i的最大和
vector<int> dfs(TreeNode* root) {
if (nullptr == root) {
return vector<int>(k + 1);
}
auto lVal = dfs(root->left);
auto rVal = dfs(root->right);
auto dp = vector<int>(k + 1);
// 枚举左右的所有状态
for (int i = 0; i <= k; i += 1) {
for (int j = 0; j <= k; j += 1) {
// 不染色
// 都贡献到dp[0]
dp[0] = max(dp[0], lVal[i] + rVal[j]);
// 染色
// 左右子树+当前节点连续染色
// 符合[1, k]
int sum = i + j + 1;
if (sum <= k) {
dp[sum] = max(dp[sum], lVal[i] + rVal[j] + root->val);
}
}
}
return dp;
}
public:
int maxValue(TreeNode* root, int k) {
this->k = k;
auto dp = dfs(root);
return *max_element(dp.begin(), dp.end());
}
};🏷️LCP 64. 二叉树灯饰
💀💥究极分类讨论
题意与思路
「力扣嘉年华」的中心广场放置了一个巨型的二叉树形状的装饰树。每个节点上均有一盏灯和三个开关。节点值为 0 表示灯处于「关闭」状态,节点值为 1 表示灯处于「开启」状态。每个节点上的三个开关各自功能如下:
- 开关
1:切换当前节点的灯的状态; - 开关
2:切换 以当前节点为根 的子树中,所有节点上的灯的状态; - 开关
3:切换 当前节点及其左右子节点(若存在的话) 上的灯的状态;
给定该装饰的初始状态 root,请返回最少需要操作多少次开关,可以关闭所有节点的灯。

注意三种操作,对左右节点的状态变化是一样的。(核心转移条件)
基本思路与968. 监控二叉树差不多。
本题可以耗死脑细胞,建议直接cv。
Code
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
template <typename T, typename... Args>
T min(T num, Args... args) {
if constexpr (0 == sizeof...(Args)) {
return num;
} else {
return std::min(num, ::min(args...));
}
}
class Solution {
private:
// 全亮
// 全不亮
// root亮,子树均不亮
// root不亮,子树均亮
tuple<int, int, int, int> dfs(TreeNode* root) {
if (nullptr == root) {
return {0, 0, 0, 0};
}
auto [lAll, lAllNot, lWithRoot, lWithoutRoot] = dfs(root->left);
auto [rAll, rAllNot, rWithRoot, rWithoutRoot] = dfs(root->right);
int all = 0, allNot = 0, withRoot = 0, withoutRoot = 0;
// !!!注意,左右子树是同步变化的!!!
// 当前本身就亮
if (root->val) {
all = min(
lAll + rAll,
lAllNot + rAllNot + 2,
lWithRoot + rWithRoot + 2,
lWithoutRoot + rWithoutRoot + 2
);
allNot = min(
lAll + rAll + 1,
lAllNot + rAllNot + 1,
lWithRoot + rWithRoot + 1,
lWithoutRoot + rWithoutRoot + 3
);
withRoot = min(
lAll + rAll + 2,
lAllNot + rAllNot,
lWithRoot + rWithRoot + 2,
lWithoutRoot + rWithoutRoot + 2
);
withoutRoot = min(
lAll + rAll + 1,
lAllNot + rAllNot + 1,
lWithRoot + rWithRoot + 3,
lWithoutRoot + rWithoutRoot + 1
);
}
// 当前节点不亮
else {
all = min(
lAll + rAll + 1,
lAllNot + rAllNot + 1,
lWithRoot + rWithRoot + 3,
lWithoutRoot + rWithoutRoot + 1
);
allNot = min(
lAll + rAll + 2,
lAllNot + rAllNot,
lWithRoot + rWithRoot + 2,
lWithoutRoot + rWithoutRoot + 2
);
withRoot = min(
lAll + rAll + 1,
lAllNot + rAllNot + 1,
lWithRoot + rWithRoot + 1,
lWithoutRoot + rWithoutRoot + 3
);
withoutRoot = min(
lAll + rAll,
lAllNot + rAllNot + 2,
lWithRoot + rWithRoot + 2,
lWithoutRoot + rWithoutRoot + 2
);
}
return {all, allNot, withRoot, withoutRoot};
}
public:
int closeLampInTree(TreeNode* root) {
return std::get<1>(dfs(root));
}
}; // 简单解释
// 当root是亮的状态下
if (root->val) {
all = min(
lAll + rAll, // 两个子树均满;则不用格外操作
lAllNot + rAllNot + 2, // 两个子树均满;则两步,全反转 + root单个反转
lWithRoot + rWithRoot + 2, // 两个子节点亮,其余均不亮;则两步,反转root和子节点 + 全反转
lWithoutRoot + rWithoutRoot + 2 // 两个子节点不良,其余均亮;则两步,反转root和子节点 + root单个反转
);
}
// 其余所有的类似讨论转移


